基于矩阵束方法的无源互调定位算法

在基于波矢k 空间傅里叶变换定位算法中，对于相近的PIM 源的分辨率或小尺度微波部件下的PIM 源位置定位会受到带宽的限制，因此在窄带条件下，往往无法实现PIM 源的定位。在波矢k 空间逆问题优化定位算法中，在已知所有PIM 隐患点位置的先验条件下，通过构造目标函数以最速下降法来获得最优解参数，通过幅度阈值条件来判断各PIM 隐患点是否真正产生PIM。但是，该算法需要已知所有可能的PIM 隐患点的数量及位置信息，对于一些复杂的微波部件（或系统），该算法的应用也受限。针对这个问题，本节介绍一种基于矩阵束方法的PIM 定位算法，实现在不需要先验条件（PIM 隐患点数量及位置）支撑下，准确判断PIM 发生点的位置信息和幅度，有效地解决多个PIM 源的定位问题，且对噪声具有一定的鲁棒性。其具体步骤如下。

第1 步，在同一参考信号源下，将两路相干信号注入待测微波腔体，在多个PIM 源处分别产生PIM 信号。特定阶数的多个PIM 信号经过反射，在入射端口叠加，其叠加合成后可视为一个多载波信号，通过幅度相位比较器可以获得叠加信号的幅度A 和相位φ，记为Aejφ。

对其中一路相干信号的频率进行等间距扫频，其中总扫频点数为m，对于第i 次扫频，获得一系列幅度A（i）和相位φi，记为

式中，k——最低频率所对应的波矢量；

Δk——扫频间隔带宽所对应的波矢量。

第2 步，经过等间隔扫频后，得到一系列单频复数信号，形式如下：

式中，y（i），y（k＋iΔk）——加噪信号；

x（i）——不带噪声的信号；

n（i）——噪声信号；

M——PIM 源数量；

An——复幅度；

zn——极点。(www.xing528.com)

由上述加噪信号构造Hankel 矩阵Y：

式中，l——矩阵束参数，范围为［m/3，m/2］。

对Hankel 矩阵Y 采用以下公式进行奇异值分解（SVD），获得Hankel 矩阵Y 的奇异值矩阵Σ，即

式中，U，V——YYH 的特征值和YHY 的特征值，V′ ＝［v1v2… vM… vl］，表示V 的矩阵转置。

将Σ 与PIM 发生阈值进行比较，获得待测器件内实际产生PIM 的PIM 源数，矩阵内高于PIM 发生阈值的奇异值则认为实际产生了PIM，否则认为不产生PIM，由此获得PIM 源的数量M。其中，PIM 发生阈值为相对于奇异值矩阵Σ 内最大值的比值。

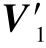通过矩阵束方法来求解矩阵束的广义特征值，从而可求得极点zn，其中 ＝［v1v2… vM－1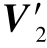］， ＝［v2v3… vM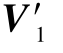］，和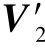 分别为V′的第1 ～M－1 列矩阵和第2 ～M 列的矩阵。

根据极点zn，利用以下公式来获得发生PIM 的位置xn：

采用最小二乘法获得PIM 发生点的幅度，有

式中，A1，A2，…，AM——产生PIM 的PIM 源x1，x2，…，xM处的复幅度大小。

基于矩阵束方法的定位算法不需要可能的PIM 隐患点数量及位置信息，即可获得所有可能产生PIM 的源点位置及其相对幅度，并准确判断PIM 发生点的位置信息，从而有效地解决多个PIM 源的定位问题。

基于矩阵束方法的定位算法流程框图如图4－9 所示。