网状天线电磁多尺度等效分析的优化方法

多尺度电大尺寸工程问题是指电磁工程问题的宏观规模达到几十乃至几百个电波长，但其中存在几十分之一波长尺度上的微观结构，这些微观结构虽然尺度很小，却因数量规模巨大、材料（或结构）特殊，导致其对电磁问题的宏观特性的影响不可忽略。

对于典型的具有松散连接结构（如网状天线），其网格尺度均在几十分之一波长以下，电性能则需要在几十个乃至上百个波长尺度的范围内进行求解。多尺度电磁结构中的微观结构的剖分密度远大于其他部分，导致矩阵的条件数恶化，在求解中收敛很慢，甚至不收敛。丝网结构会造成电磁波因绕射效应而泄露，而丝网节点处的金属结的非理想接触会引起网状天线的PIM。该结构属于典型的多尺度、非线性PIM 的电大尺寸电磁问题。

多尺度电磁工程问题无法利用现有的数值计算方法（如有限元、矩量法及其快速算法等）进行几何剖分运算，会导致矩阵求解无法收敛，甚至连几何剖分都无法完成。但是，微观结构由于数量规模、材料、结构等原因，其宏观影响必须通过数值计算来进行分析、评估。等效方法是解决这一矛盾的有效手段。等效方法是指将微观结构对于宏观结构中电磁行为的影响以边界条件的形式等效，并加入宏观结构进行求解。这种等效方法将问题分为两个阶段：在第1 阶段，研究微观结构的电磁响应，并将其等效为边界条件；在第2 阶段，解决不含有具体微观结构但含有其等效边界条件的宏观电磁问题。多尺度问题的等效方法化难为易，解决了直接求解方法中的数值离散化带来的计算难题，且充分考虑了微观结构的电磁效应。具有松散接触的周期性微观结构（如丝网反射面、频率选择表面、天线罩高频段特性分析等）的多尺度电大尺寸问题均可采用等效分析方法来进行数值分析。

美国的Rahmat－Samii 等人应用Floquet 方法研究了不考虑电接触模型（即理想搭接）情况下周期性反射面天线（mesh antenna）的特性，主要研究了周期结构单元的尺寸和形状等因素对于反射特性的影响。对于搭接的影响，以理想连接和完全断开两种极端情况作为极限来进行评估。毛煜茹、谢拥军等人采用的多尺度等效分析方法对松散连接的周期性单元结构进行电磁建模，并在金属结处引入金属搭接的电接触模型等效的RLC 边界条件，采用Floquet 方法来求解周期平面结构的电性能参数。这种网状天线多尺度等效方法的计算流程如图3－25 所示。

图3-25　网状天线多尺度等效方法的计算流程

1.网状天线金属丝接触建模分析

实际上，金属与金属之间的接触并非完全光滑表面的接触，而是在接触面上具有一定粗糙度的面接触。金属表面的粗糙度是指由于机械加工而在金属加工表面上分布的一些微小间距和峰谷共同构成的微观几何形状特性。这样，金属－金属间的接触实际上是发生在金属表面的峰和谷的接触，也可以将其理解为是一些凸起部分与凹陷部分的多种接触情况的综合。接触面暴露在空气中，表面生成氧化层或吸附污染物，形成MIM（Metal Insulator Metal，金属－绝缘体－金属）结构，粗糙接触切面如图3－26 所示。图3－26 中有5 种接触状态：①金属接触；②接触面之间夹有金属氧化膜；③接触面之间夹有绝缘介质；④微小空气间隙；⑤较大空气间隙。①和②形成电流的主要通道，形成收缩电阻和接触电阻；②中的氧化物依靠隧道效应和穿透薄膜的金属桥进行导电，属于半导体接触导电，是非线性的；③不导电，电流绕到金属接触处通过；在空气间隙（④和⑤），电流环绕间隙流过。当电流遇到阻抗Z 时，就产生间隙电压，间隙电压是潜在的，可能激活任何一个非线性效应，从而产生PIM 效应。

图3-26　粗糙接触面切面

金属接触的等效电路模型如图3－27 所示，实际接触区域的电容为Cc，非接触区域的电容为Cn－c，接触电阻为Rc。

图3-27　金属接触的等效电路模型

金属接触受外力载荷后，将微观接触区近似为面接触。对于粗糙表面的接触研究，将直接作用于接触面的电性能研究。采用GW 模型来研究两个粗糙表面的接触状态时，将其中一个粗糙表面看作理想光滑硬平面，将另一个粗糙表面看作符合微凸体分布规律假设的粗糙面。这样引入等粗糙度表面的假设，就可以简化实际接触面积的计算。将两个接触表面的粗糙度叠加到一个等效平面后，就可以将问题简化为一个理想光滑硬平面与一个等效粗糙平面的接触分析。等效后的接触模型如图3－28 所示，粗糙表面的微凸体部分参与接触，压入光滑硬平面，产生接触面积，承受接触载荷；部分不参与接触，不产生接触面积。

图3-28　金属表面接触的GW 模型

在图3－28 中，l 表示微凸体凸峰压到硬平面上产生的微凸体径向变形量；d 表示粗糙表面上所有微凸体的平均高度参考线距理想光滑硬平面的距离；z表示微凸体高度。此外，An表示名义接触面积；Areal表示实际接触面积；接触面粗糙度参数β ＝ησr，η 表示微凸体分布密度，σ 表示微凸体高度标准差；r表示微凸体半径；假设所有微凸体高度相等且分布概率密度函数φ（z）服从高斯分布。

无量纲实际接触面积A* ＝Areal/An的计算公式如下：

式中，Iα 的表达式为

式中，无量纲微凸体平均高度d* ＝d/σ；无量纲微凸体高度z*的概率密度函数φ*（z*）的表达式为

式中，σs——微凸体等效表面高度标准差。

无量纲临界变形量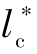 ＝lc/σ，lc的表达式为

式中，K ＝0.454＋0.41v，v 为材料的泊松比；

H——材料硬度；

E——赫兹弹性模量。

接触面上受到接触载荷后，微凸体将进入接触状态，接触载荷决定了参与接触的微凸体数Nc，其表达式为

因此，图3－27 中非接触电容Cn－c的表达式为

接触电容Cc的表达式为(https://www.xing528.com)

式中，εr——绝缘层的相对介电常数；

s——绝缘层的厚度。

接触电阻Rc的表达式为

式中，；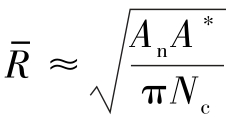

ρM1，ρM2——两种接触材料的电阻率。

2.网状天线周期编织结构电磁分析

由于编织结构的金属网具有周期性，因此利用基于有限元法实现的Floquet模式展开求解金属网上的电磁波是一种有效的求解方法。周期有限元法允许通过仅分析周期单元来实现无限大平面的求解。首先，建立一个由周期性边界条件约束的周期性单元模型，并使用周期有限元法来获得无限大平面的反射系数。以下公式中的dx和dy是周期性参数。对于周期性结构，电磁场满足Floquet 定理的周期性条件。那么，散射场ES和透射场ET可以写为

散射场远场仅由TE 和TM 模式组成时，则其中p ＝0 和q ＝0；否则，可能存在高次模，p ＝0 和q ＝0 对应主模式，p≠0 和q≠0 对应于高次模。高次模式是渐逝模式，且场随距离增加而快速降低。下标m 为1 或2，分别用于表示TE 模式、TM 模。Rmpq和Bmpq分别表示周期结构的反射系数和透射系数。

所得的TE 和TM 矢量模式函数ψmpq具有以下形式。

式中，

电磁波入射金属网平面，k 是传播常数，入射方向为（θ，φ），则

式中，

金属网的电性能在很大程度上取决于这些金属丝接触点的接触情况。任何阻碍电流流经这些结的因素都会导致反射性能的变差。因此，在金属网表面建模中应考虑导线交叉接触的影响。为正确模拟接触状态，如图3－29 所示，在接触点的接触区域上施加集总边界条件（集总边界条件等效电路如图3－27 所示），从而实现金属网表面电磁场的精确求解。

图3-29　具有MIM 结构的电接触模型的金属网周期结构电磁模型

3.仿真实例

使用电磁多尺度等效方法分析正馈抛物反射面天线，抛物面直径为0.6 m，焦距为0.4 m。角锥喇叭位于反射面焦点，馈源喇叭驻波比VSWR 为1.2，工作频率为8 GHz，极化方式为线极化。由3.5.1 节第一部分中的公式计算网状反射面接触结等效电路的集总参数，Rc≈50 Ω，Cn－c≈56 pF，Cc＝25 pF。

将图3－29 所示的编织结构接触结处的接触状态用三种状态来表征，分别为理想接触（Perfect－computed）、无接触（Broken－computed）和集总边界加载（Lumped－computed）。利用周期有限元法可以得出金属网反射损耗S11，如图3－30 所示。

图3-30　不同接触状态金属网反射系数

图3－31 给出了不同接触模型的反射面天线的远场辐射方向。固体反射面与网状天线的材料相同，金属网由铜线编织而成。实线表示固体反射面天线的辐射方向，虚线和带圆圈的实线分别表示在金属丝接触结点处的完美连接和集总连接。

表3－1 列出了这些反射面天线的最大方向性。由表可知，在8 GHz 时，集总连接反射面天线的最大方向性与固体反射面和理想接触反射面相比分别降低了0.9 dB 和0.6 dB。在网状反射面天线的实际应用中，金属网的电性能特征很大程度上取决于这些金属丝接触结处的接触状态，建立适当的网状编织单元模型有助于实现网状反射面天线的性能的精确分析，精确的电性能分析是PIM 分析的基础。

图3-31　不同接触模型的反射面天线的远场辐射方向图（8 GHz）

表3-1　反射面天线的最大方向性