根据经典接触力学，采用三个主要的参量（微凸体面密度η、微凸体高度标准差σ 和微凸体半径R）来描述微波部件表面形貌，这三个参数可以从LSM（激光扫描显微镜）或AFM（原子力显微镜）的三维形貌数据中提取。在接触力学的经典模型——GW（Greenwood Williamsons）模型中，两个粗糙表面的接触等效为一个光滑刚性平面与一个具有等效参数的粗糙表面的接触，如图2－13 所示。
图2-13 粗糙表面接触等效GW 模型示意图
等效参数与原始粗糙表面形貌参数的关系如表2－2 所示。单个微凸体的变形模型示意如图2－14 所示。
表2-2 等效参数与原始粗糙表面形貌参数的关系
图2-14 单个微凸体的变形模型示意
z—微凸体的高度
采用M.R.Brake 提出的模型来计算单个微凸体的变形过程，计算公式如表2－3 所示。采用Ag 的力学参数对等效半径R ＝45 μm 的微凸体的变形过程进行计算，结果如图2－15 所示。
表2-3 单个微凸体力学计算模型
图2-15 单个微凸体的变形过程
当基于前述单个微凸体接触理论获得了单个微凸体的接触面积与接触压强后，粗糙表面的接触面积与接触压强可采用如下的积分式得到。(www.xing528.com)
粗糙表面的接触面积：
粗糙表面的接触压强：
粗糙表面的接触微凸体数目：
式中，η——微凸体的面密度；
An——名义接触面积；
d——刚性平面与等效粗糙面表面高度均值间距。
这样，当接触的粗糙表面具有不同的微凸体形貌时，只需对单微凸体的接触面积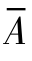
、接触压强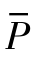
进行相应的计算，便可通过类似的积分计算来获得接触特性。
上述积分方法采用的是统计的方法，当样本数量较多，并且样本特征服从给定的分布时，该方法是有效的。但对于实际微波部件，由于对部件特性起主要作用的往往是接触截面边缘的一部分微凸体，这部分微凸体的个数是有限的，且由于部分微凸体是MM（Metal－Metal）接触，不产生非线性，因此产生非线性的微凸体个数就更少了，此时非线性将有一定的随机性，这是无法采用积分方法描述的。另外，如果考虑非理想因素（如微凸体形状、微凸体半径的分布和摩擦等因素），积分的方法将使计算变得越来越复杂。因此这里采用蒙特卡罗法，对每个微凸体单独计算，从而使得分析过程变得简单，并且能够很方便地引入非理想因素。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
