MOM结构界面势垒模型和载流子输运机制的优化方法

在实际的微波部件金属镀层自然低温氧化过程形成的氧化膜中，存在一定浓度的施主和受主缺陷。接下来，根据氧化物中存在的缺陷类型，分情况讨论分析基于金属表面超薄氧化层的MOM（Metal－Oxide－Metal）结构的势垒模型、模型参数以及主要的输运方程。

2.2.2.1　氧化层中以施主型缺陷为主的MOM 结构分析

在此，以银表面形成Ag2O 为例进行分析。在Ag2O 形成过程中产生的缺陷有Ag 间隙、氧空位以及杂质浅施主等，其中浅施主缺陷电离成n 型半导体，相比于本征半导体，费米能级EF向导带底靠近，金属功函数大于氧化物功函数，在这种情况下，MO（Metal Oxide）界面形成肖特基接触势垒，隧穿电流和肖特基热发射电流为主要电流机制。这里给出弱n 型Ag2O MOM 结构的热平衡势垒模型及其在偏置电压（简称 “偏压”）条件下的势垒模型，如图2－2所示。

对于弱n 型氧化物，可近似视为介质层，外加电压下氧化层中为匀场；对于强n 型氧化物，氧化层耗尽区能够屏蔽电场，在外加电压较小的条件下，将主要降落在反偏的界面上，耗尽层向氧化物中展宽，在薄氧化层条件下也可近似为匀场条件。

在不考虑镜像力效应的条件下，有

图2-2　热平衡和偏压条件下弱n 型Ag2O MOM 结构的势垒模型

（a）不加偏压；（b）加偏压
EC—导带能级；EF—费米能级；EV—价带能级

式中，φbn——考虑镜像力效应的势垒高度；

φm——金属和半导体接触的势垒高度；

χox——氧化物的电子亲和能。

根据固体电子学中热电子发射理论，得到MOM 结构的热电子发射电流公式为

式中，Va——偏置电压（V）；

A——有效理查逊常数，取值为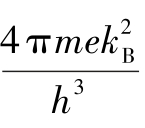，m 为电子质量，kB为玻尔兹曼常数，h 为普朗克常数；

T——温度（K）；

φb0——MOM 结构不考虑镜像力效应下的势垒高度（eV）。

在考虑镜像力效应的条件下，则得到更准确的热电子发射电流公式为

Simmons 假设在外加偏压条件下，空间电荷限制效应可以忽略、氧化物接触电极间的场强足够大，且两电极间氧化物上的电场分布为匀场条件，得到了经典的Simmons热电子发射电流公式。按照Simmons 理论，MOM 结构的热电子发射公式为

式中，εox——氧化层的相对介电常数；

tox——氧化层的厚度。

即在Simmons 理论中，镜像力势垒降低效应约为

事实上，我们所研究的金属表面自然氧化形成超薄氧化物后接触界面的MOM 结构，并不满足Simmons 理论中的假设条件，即弱场下的热发射电流和后面的隧穿电流对接触非线性理论分析是必不可少的。Simmons 理论中的镜像力势垒降低效应的推导经过了近似和拟合，我们采用的是Simmons 理论之后基于库仑作用发展起来的较为准确的镜像力势垒降低效应模型。如图2－3 所示，在匀场条件下氧化物中的势函数为

式中，x——以金属－氧化物为起始的氧化层中的位置；

－——根据镜像电荷库仑作用推导而来的势函数，ε0为真空介电常数；

E——电场强度，

图2-3　金-半接触势垒降低原理

（a）电荷镜像原理示意；（b）金－半接触势垒模型；（c）考虑镜像力的金－半接触势垒模型

根据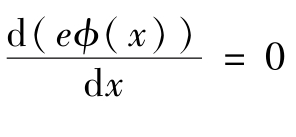，求得xm处为势垒最高位置，即

从而得到镜像力导致的势垒降低幅度为

将其代入式（2－3），得到考虑镜像力效应的热电子发射电流公式为

以Ag2O 的参数为例进行分析，在tox＝10 nm、Va＝100 mV、εox＝3.2 条件下，xm＝3.35 nm。

事实上，式（2－9）只有在xm≤tox的条件下（即氧化层足够厚的条件下）才成立，此时热电子发射电流公式（式（2－10））必须满足条件xm≤tox，即只有在的外加偏压下才成立。实际上，自然形成的氧化层很薄，当满足xm＝的条件时，势垒降低幅度为

将其代入式（2－10），得到

热发射电流过程（图2－4）对氧化物势垒高度及外加偏压的依赖性较强，相比之下，根据量子隧穿理论计算MOM 结构的氧化层薄势垒的电子隧穿过程不仅依赖于氧化物势垒高度，而且对势垒形状（即势垒沿着隧穿方向的函数）具有强烈的依赖性。根据基于WKB［J］近似（WKB［J］ approximation）的Simmon理论，可得出外加偏压Va下隧穿电流的通用表达式，即

式中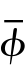，——加负压的左电极的费米能级之上的势垒高度平均值。

式中，s1，s2——氧化层两边的位置。

图2-4　热发射电流密度J-V 特性(www.xing528.com)

（a）不同接触电势对电流密度的影响；（b）不同氧化层厚度对电流密度的影响

图2-4　热发射电流密度J-V 特性（续）

（c）不同温度对电流密度的影响

如图2－5 所示，式（2－13）中的第一项可看作由左电极流到右电极的电流，第二项则为右电极流到左电极的电流，二者相减得到在偏压Va条件下左电极流入右电极的净量子隧穿电流。

图2-5　在加偏压条件下势垒与电流的变化情况

考虑镜像力和氧化物层上场分布为匀场的条件，Simmons 给出了量子隧穿电流计算公式，即

式中，

式中，s——以金属－氧化层界面为起始，在氧化层中的位置。

另外，由于射频连接接触非线性电流往往是一个极弱的信号，因此还需要考虑极小电压下的J－V 关系，即在Va≈0 条件下，

式中，

事实上，在极小电压下，J－V 是线性的，如图2－6 所示。也就是即使MOM 结构上存在隧穿电流，在接触结上阻抗较小的条件下，界面氧化物依旧类似一个线性电阻，如果微波部件接触阻抗满足该条件，那么这种条件下需分析产生PIM 的其他非线性特性。

图2-6　隧穿电流J-V 特性曲线

（a）不同势垒高度对电流密度的影响

图2-6　隧穿电流J-V 特性曲线（续）

（b）不同氧化层厚度对电流密度的影响

2.2.2.2　氧化层中以受主型缺陷为主的MOM 结构势垒模型及其输运方程

Ag2O 中的受主型缺陷主要是在氧化银的制备过程中形成的银空位和引入的受主杂质。当Ag2O 中存在大量受主型缺陷时，称为一个p 型半导体。在弱p 型条件下，随着空穴浓度的增加，金属功函数φm从大于氧化物功函数φox向与氧化物功函数相等变化。根据半导体理论，在φm＞φox的条件下，金属和氧化物界面形成p 型反阻挡层，如图2－7 所示。

图2-7　金属和氧化物界面形成p 型反阻挡层过程示意图

反阻挡层实际上是很薄的高电导层，它对氧化物和金属的接触电阻影响很小。也就是说，在外加偏压条件下，氧化层上的电导过程不再受电极接触势垒的影响，而由体过程控制。其电流密度JL0与电场强度E 的依赖关系为

式中，σ0——电导率，σ0＝poxeu，

式中，NV——价带有效状态密度，

如果近似取室温下NV＝2.5 ×1019/cm3，那么

取u ＝100 cm2/（V·s），可得到室温下的电流密度为

即在室温下，J－V 为线性依赖关系。但是，电导率是温度的函数，温度越高，本征载流子的浓度就越大，同时在仅考虑晶格声子散射的条件下，温度越高，迁移率就越低。电导率对温度的非线性依赖关系可能导致电热耦合效应。

随着氧化银层中空穴浓度的增加，费米能级向价带顶靠近，其费米能级EFp对空穴浓度的依赖规律为

式中，p0——空穴浓度。

在强电离条件下，p0≈NA

式中，NA——Ag2O 中的受主浓度。

氧化物的功函数φox为

式中，χ——Ag2O 的电子亲和势；

Eg——禁带宽度。

当氧化物中的空穴浓度大于8.23 ×1010/cm3 时，金属的功函数小于氧化物功函数，根据半导体理论，p 型氧化物和金属的MO 界面形成阻挡层。下面给出在φm＝φox＝4.5 eV，p 型氧化银和金属的MO 界面形成阻挡层，且热平衡的条件下，MOM 结构势垒模型和偏压下的MOM 结构势垒模型，如图2－8 所示。

图2-8　p 型氧化银的MOM 结构势垒模型

空穴势垒的高度φbp由下式确定：

对于微波部件镀银层的自然氧化过程包括氧化过程中形成银空位，根据低温氧化动力学过程初步判断低温热氧化形成的Ag2O 中存在从金属－氧化层到氧化层－大气的银空位分布，具体要根据可控低温氧化过程实验研究确定。