比较众数、中位数和均值的差异

（一）众数、中位数和均值的关系

1.对称分布：=Me=Mo

在单峰分布条件下，当数据呈正态分布时，总体内次数分布两边呈完全对称的钟形曲线，算术平均数、中位数和众数处于同一位置上，三者重合。

2.右偏：Mo＜Me＜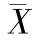

当数据呈现右偏态分布时，说明数据出现极大值，必然将算术平均数拉向极大值方向，中位数也相应增大，众数依然保持不变，表现为＞Me＞Mo。

3.左偏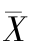：＜Me＜Mo

当数据呈现左偏态分布时，说明数据存在极端的小值，必然将算术平均数拉向极小值方向，中位数也相应减小，而众数依然保持不变，于是有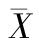＜Me＜Mo。

4.三者数量关系(www.xing528.com)

著名统计学家卡尔·皮尔逊的研究结果表明，在钟形分布只存在轻度偏斜的情况下，不论是右偏还是左偏，算术平均数、中位数和众数三者的关系是：算术平均数与众数的距离约等于算术平均数与中位数距离的三倍，即

（二）众数、中位数和均值的特点和应用场合

众数不受极端值影响，具有不唯一性，数据分布偏斜程度较大时应用。

中位数不受极端值影响，数据分布偏斜程度较大时应用。

平均数易受极端值影响，数学性质优良，数据对称分布或接近对称分布时应用。

此外，均值只适用于定距或定比尺度的数据，而对于定类或定序尺度的数据则无法计算均值，但却可以计算众数和中位数，对定距和定比尺度的数据也同样适合于计算众数和中位数。