【摘要】：均值是全部数据的算术平均，也称为算术平均数。（一）简单算术平均数若资料未分组，计算算术平均数可招各单位标志值直接相加，再除以总体单位数，所得的平均数称为简单算术平均数。其计算公式为式中，表示算术平均数；Xi表示变量值；n表示总体单位数。影响加权算术平均数的因素有两个，一个是各组变量值X，一个是各组次数f。
均值是全部数据的算术平均，也称为算术平均数。均值在统计学中具有重要的地位，是集中趋势的最主要测度值。
算术平均数根据掌握的资料不同和计算的复杂程度，可分为简单算术平均数和加权算术平均数。
（一）简单算术平均数
若资料未分组，计算算术平均数可招各单位标志值直接相加，再除以总体单位数，所得的平均数称为简单算术平均数。其计算公式为
式中，
表示算术平均数；Xi表示变量值；n表示总体单位数。
特点：简单算术平均数的大小只受各变量值本身大小的影响，其平均数的大小不会超过变量值的变动范围。
（二）加权算术平均数
若资料是经过分组的变量数列，应采用加权平均的方法计算其平均数。计算公式为
式中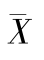
表示算术平均数；Xi表示各组组中值；fi表示各组单位数（权数）。
影响加权算术平均数的因素有两个，一个是各组变量值X，一个是各组次数f。各组变量值次数f的多少对平均数的影响有权衡轻重的作用，所以f又称为权数。(www.xing528.com)
权数大的变量值对平均数的影响要大些，反之，则小些。
若各组权数都相等，权数所决定的各组变量值的作用都一样，便失去了权数的意义。这时，加权算术平均数等同于简单算术平均数。
（三）算术平均数的数学性质
1.各个变量值与其算术平均数的离差之和等于零
简单算术平均数：Σ（Xi-
）=0
加权算术平均数：Σ（Xi-
）fi=0
2.各个变量值与算术平均数离差之和等于最小值
简单算术平均数：Σ（Xi-
）2=min（最小值）
加权算术平均数：Σ（Xi-
）2fi=min（最小值）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
