中位数的计算及其应用

中位数是将总体各单位的标志值按大小顺序排列，处于数列中点位置的标志值为中位数，常用Me表示。中位数将数列分为相等的两部分，一部分的标志值小于中位数，另一部分的标志值大于中位数。因而，中位数能够反映社会现象的一般水平和集中趋势。

根据所掌握的资料是否分组以及分组的情况，中位数的计算有四种情况。

（一）由未分组数据确定中位数

根据未分组资料确定中位数时，首先将标志值按大小顺序排列，然后根据公式（n+1）/2确定中位数的位置，再根据中位数的位置找出对应的标志值。如果总体单位数n为偶数，则取中间位置上的两个变量值的简单算术平均数为中位数。

（二）由分组数据确定中位数

第一步，先求中位数的位置；第二步，计算累计次数；第三步，确定中位数所在组；第四步，运用公式计算中位数的近似值。

中位数的计算公式(www.xing528.com)

下限公式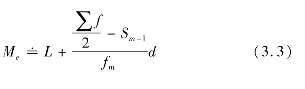　

上限公式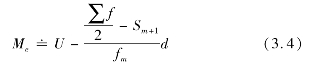　

式中，L表示中位数组的下限；U表示中位数组的上限；fm表示中位数组的次数；Sm-1表示中位数所在组以前各组的累计次数；Sm+1表示中位数所在组以后各组的累计次数；∑f表示总次数；d表示中位数所在组的组距。

上面两个公式计算的结果完全相同。需要说明的是，利用上述公式计算中位数，是假设中位数组内的变量值是均匀分布的，因此计算结果只能是中位数的近似值。

中位数的特点：位置均值，不受极端数值的影响，具有稳健性的特点。此外，中位数还具有这样一个性质，这就是各变量值与中位数的离差之和最小。

应用场合：数据存在明显的集中趋势时。