在传统的计划网络中,关键路径是网络中从开始节点到结束节点之间的最长路径。其节点与工序都不具有机动时间,即最早时间与最迟时间相等,前一个工序一结束下一个关键工序就需要马上开始。一旦关键路径上的工序出现延迟就会影响到整个网络项目的进度,使项目的总工期延长。而在时间转换约束的条件下,由于工序本身可能受到开始时间的约束,当前工序在最早时间结束,并不意味着紧后工序就能马上开始。在当前工序最早结束时刻与紧后工序最早开始时刻之间可能存在间隔时间,而这些间隔时间对于当前工序来说可能就是可以利用的自由时差。
如图7-2所示,在情况1中,当前工序为dnw-pattern,结束于星期五的白天,而紧后工序为day-pattern,只有等到下周周一的白天才能开始。那么,当前工序就具有5个工时的自由时间。又如在情况2中,当前工序为d&n-pattern,结束于周四白天,而紧后工序为day-pattern,在周四晚上不能马上开始,必须等到周五的白天才能开始,那么,当前工序就有一个工时的自由时间。如果这两个工序都在关键路径上,那就意味着关键工序也可能有机动时间。
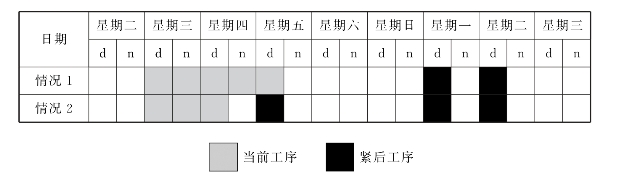
图7-2 不同类型工序的进度安排(https://www.xing528.com)
时间转换约束除了可以使关键路径出现机动时间外,还有可能使关键路径发生变化,使原来的关键工序变成非关键工序,使原来的非关键工序变成关键工序。这是由于时间转换约束模型使工序的开始时间以及持续时间发生变化所造成的。
如图7-3所示,l为关键路径,实际耗时为20个工时,工序a的实际耗时为4个工时,工序b的实际耗时为9个工时。如果l为dnw-pattern,工序a为d&n-pattern,工序b为day-pattern。在周一白天开始的情况下,路径l将在下一周的周三晚上结束,工序a将最早在本周的周二晚上结束,而工序b将最早在本周三的白天开始,并最早结束于第三个星期的周一白天。显然,工序a与工序b所组成的路径取代了路径l成为了关键路径,网络的持续时间也变成了29。综上所述,与传统计划网络相比,在时间转换约束模型下,关键路径有可能会有机动时间,也有可能因为受工序类型的影响而发生变化。
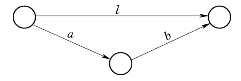
图7-3 关键路径的改变
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




