优化亏值的算法方法

三个平行序链顺序优化问题的优化过程可以表述为：比较6个最小亏值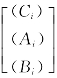，，，，，大小，最小值所对应的调整顺序就是最佳的，即三个工件在这n台机器上的加工顺序也是最佳的。现在问题的关键是6个最小亏值的算法。我们只需给出其中一个亏值的算法，其余5个可类似得到。

假设这三个平行序链的第一个平行工序调整为A1→B1→C1。

由于三个平行序链的第一个平行工序调整为A1→B1→C1，相当于这个网络图在原路线的基础上增添了三类新路线，过A1→B1的路线，过B1→C1的路线，以及过A1→B1→C1的路线，新增路线的最大路长是max{，，}。

接下来就是其他平行工序的调整。这里假设机器没有中断时间，在把三个平行序链的第二个工序调整为顺序工序时，工序A2必然先开始做。若A2的工期比B1的工期与C1的工期和还要大，当工序B1与C1都结束时，工序A2还没有结束，既然工序B1与C1都结束了，那么B2与C2就都可以开始了。而B2和C2又要作为A2紧后工序，所以哪个工序作为A2的紧后工序都可以，这就要求第二平行工序有两种调整方案（A2→B2→C2和A2→C2→B2），我们也分别找出调整后新增加的路线，算出每种调整方案的新增加路线的最大路长。若A2的工期比B1的工期与C1的工期的和小，这说明A2结束时C1还未结束，B1先于C1结束，这说明A2的紧后工序只能是B2，然后再到C2，只有这一种调整顺序（A2→B2→C2），我们找出调整后新增加的路线，算出每种调整方案的新增加路线的最大路长。按照三元序链的第二个平行工序的顺序调整方式逐个调整接下去的工序，每一步都需要计算出新增路线的最大路长，直到第n步。自然找到了所有的可行方案，找到了每个可行方案新增加路线的最大路长，也就计算出了亏值。

的算法如下。

（1）三个平行序链的第一个工序调整为A1→B1→C1，计算，，的值，并比较大小，取其最大值。

（2）若TA2＜TB1+TC1，三个平行序链的第二个工序调整为A2→B2→C2，则需计算，，的值，并比较大小，取其最大值；若TA2＞TB1+TC1，三个平行序链的第二个工序调整为A2→B2→C2或A2→C2→B2。

1）若第二个工序的顺序调整为A2→B2→C2，则需计算，，，的值，并比较大小，取其最大值。

2）若第二个工序的顺序调整为A2→C2→B2，则需计算，，，，，的值，并比较大小，取其最大值。

（3）以此类推，第i+1（i=1，2，…，n-1）步算法如下。(www.xing528.com)

1）若TAi+1＜TBi+TCi，则第i+1个平行工序的调整顺序应与第i个平行工序的调整顺序相同。

a.若第i个平行工序的调整顺序为Ai→Bi→Ci，则第i+1个平行工序的调整顺序为Ai+1→Bi+1→Ci+1。需要计算，，，的值，并比较大小，取其最大值。

b.若第i个平行工序的调整顺序为Ai→Ci→Bi，则第i+1个平行工序的调整顺序为Ai+1→Ci+1→Bi+1。需要计算，，，的值，并比较大小，取其最大值。

2）若TAi+1＞TBi+TCi，第i+1个平行工序的顺序应调整为Ai+1→Bi+1→Ci+1或Ai+1→Ci+1→Bi+1。

a.若第i+1个平行工序的顺序调整为Ai+1→Bi+1→Ci+1，需要计算，，，（与第i个平行工序的调整顺序有关）的值，比较大小，取其最大值。

b.若第i+1个平行工序的顺序调整为Ai+1→Ci+1→Bi+1，需要计算，，，（与第i个平行工序的调整顺序有关）的值，比较大小，取其最大值。

从而依次找到了三个平行序链顺序优化的所有可行方案，且得到了每个可行方案中新增加路线的最大路长。把所有可行方案的最大路长进行比较，取最小值，用最小值减去原计划的工期，就是我们所求的亏值。为了更清楚的说明上述算法，其第i+1（i=2，…，n-1）步流程如图6-6所示。

图6-6　算法的第i+1（i=2，…，n-1）步流程