优化算法：根据工序Aa时间分类工序集合

6.1.3.1　问题分析

从n个可分解平行工序中选取一个与指定工序调整为顺序工序的优化问题是指：在n个可分解的平行工序A1，A2，…，An中，选取哪个工序与指定工序Aa调整为顺序工序，推迟总工期最小，最小工期是多少？

6.1.3.2　优化算法

（1）比工序Aa最早开始时间小的工序放入集合A中，不小于工序Aa最早开始时间的工序放入集合B中，比工序Aa最迟结束时间小的工序放入集合C中，不小于工序Aa最迟结束时间的工序放入集合D中。

（2）在A∩C中选取最早结束时间（EF）小的工序放入集合Ω中；在A∩D中选取机动时间（TF）大的工序放入集合Ω中；在B∩C中选取工期（T）小的工序放入集合Ω中；在B∩D中选取最迟开始时间（LS）大的工序放入集合Ω中。

（3）计算Ω中的与Aa调整为顺序工序的亏值，选取最小亏值所对应的工序。

该优化算法如图6-4所示。

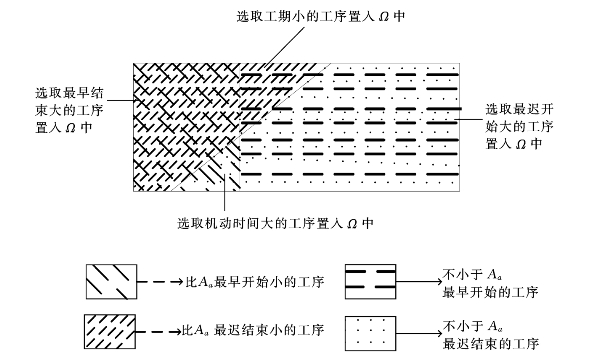
图6-4　工序优选后置入Ω中

证明　设A1，A2，…，An是n个任意可分解的平行工序，指定工序为Aa。

1）设比Aa最早开始时间小，最迟结束时间小的工序为Ai1，Ai2，…，Air，根据亏值模型，从中任意选取一个工序与Aa调整为顺序工序，推迟最小工期为

Δt=max{ESAil+TAa+TAil-LFAa,0}

=max{EFAil+TAa-LFAa,0}

其中l=1，2，…，r，因为TAa，LFAa为确定的值，所以只需选择Ai1，Ai2，…，Air中最早结束时间（EF）小的工序放入集合Ω。

2）设比Aa最早开始时间小，不小于Aa最迟结束时间的工序为Ai（r+1），Ai（r+2），…，Ai（r+m），根据亏值模型，从中任意选取一个工序与Aa调整为顺序工序，推迟最小工期为

Δt=max{ESAil+TAa+TAil-LFAil,0}

=max{EFAil+TAa-LFAil,0}

其中l=r+1，r+2，…，r+m，欲使Δt值最小，只需将Ai（r+1），Ai（r+2），…，Ai（r+m）中机动时间（TF）大的工序放入集合Ω中即可。(www.xing528.com)

3）设不小于Aa最早开始时间，小于Aa最迟结束时间的工序为Ai（r+m+1），Ai（r+m+2），…，Ai（r+m+q），根据亏值模型，从中任意选取一个工序与Aa调整为顺序工序，推迟最小工期为

Δt=max{ESAa+TAa+TAil-LFAa,0}

=max{EFAa+TAil-LFAa,0}

其中l=r+m+1，r+m+2，…，r+m+q，欲使Δt值最小，只需将Ai（r+m+1），Ai（r+m+2），…，Ai（r+m+q）中工期（T）小的工序放入Ω中即可。

4）设不小于Aa最早开始时间和最迟结束时间的工序为Ai（r+m+q+1），Ai（r+m+q+2），…，Ain，根据亏值模型，从中任意选取一个工序与Aa调整为顺序工序，推迟最小工期为

Δt=max{ESAa+TAa+TAil-LFAil,0}

=max{ESAa+TAa-LSAil,0}

其中l=r+m+q+1，r+m+q+2，…，n，欲使Δt值最小，只需从Ai（r+m+q+1），Ai（r+m+q+2），…，Ain中选最迟开始时间（LS）大的工序放入集合Ω中即可。

5）计算Ω中工序与Aa调整为顺序工序，亏值最小所对应的工序即为所求。

6.1.3.3　算例

在一个工程项目中，Z1，Z2，Z3，Z4，Z5是五个任意可分解的平行工序，现在从Z1，Z2，Z3，Z4中选取一个工序与指定工序Z5调整为顺序工序，选择哪个工序会使总工期推迟最少？

解：首先根据情况画出CPM网络图，给出各个工序的工期（图6-5），并根据图6-5给出工序Z1，Z2，Z3，Z4和Z5的时间参数表（表6-1）。

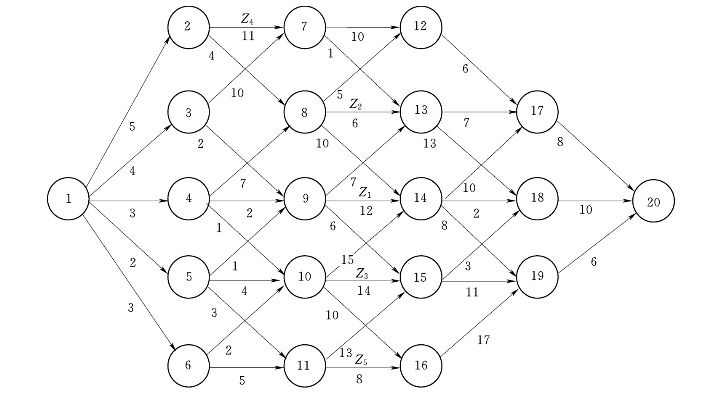
图6-5　施工网络图

表6-1　工序Z1，Z2，Z3，Z4和Z5的时间参数值

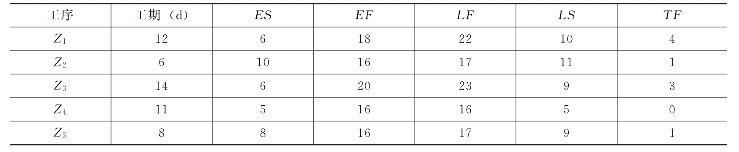
根据6.1.3.2节的优化算法，集合A={Z1，Z3，Z4}；集合B={Z2}；集合C={Z4}；集合D={Z1，Z2，Z3}，故A∩C={Z4}；A∩D={Z1，Z3}；B∩C=Ø；B∩D={Z2}，因此A∩D中选取Z1，即Z4，Z1，Z2被置入集合Ω中，Z4与Z5调整为顺序工序产生的亏值为7，Z1与Z5调整为顺序工序产生的亏值为4，Z2与Z5调整为顺序工序产生的亏值为5，因此Z1就是我们所要寻找的工序。

通过上述算例可以看出，无论从多少个可分解的平行工序选取一个工序与指定工序调整为顺序工序，集合Ω中最多不超过四个工序，因此，可以得到这样的结论，当工序个数越多的时候，该算法的优越性就越明显。