亏值模型的建立与优化

为了证明即将建立的亏值模型正确性，本节首先需要对任意可分解的两个平行工序顺序优化的方法进行分析。

6.1.2.1　优化方法分析

不妨设任意可分解的平行工序A1，A2，对孔峰等的优化方法进行改进，并对改进后的优化方法进行如下分析。

（1）若A1，A2中存在一个工序的最早可能结束时间（EF）小于或等于另一个工序的最早可能开始时间（ES）的情况，相当于这两个平行工序A1，A2之间存在一个隔断，则前者先干。

分析这种调整方式，新增路线的最大路长不会超过μ∇，故调整后网络的最大路长仍为μ∇。

（2）若两个可分解平行工序A1，A2之间不存在隔断，当把这两个平行工序A1，A2调整为一组顺序工序时，首先将最早可能开始时间小的工序A1分解顺序工序，，即为的紧前工序，并使工序的持续时间=ESA2-ESA1，即工序A2，的最早可能时间相等，然后比较工序A2，的LF，令LF小的工序为B0，LF大的工序为C0（若LF相等，令任一工序为B0，另一工序为C0），则A0→B0→C0顺序最佳。

下面讨论分解后的各种情况。

1）ESA1≤ESA2，LFA1＞LFA2，如图6-1所示。

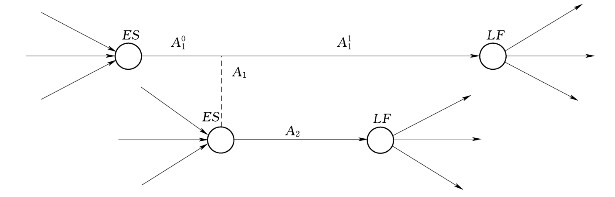
图6-1　ESA1≤ESA2，LFA1＞LFA2

根据上面陈述，最佳调整方式为→→。调整后网络有四类路线：

①原有路线；

②过→→的路线；

③过A2→的路线；

④过→A2的路线。

在这4条路线中，②中路线的最大路长为

③中路线的最大路长为

④中路线的最大路长为

因此④中路线的最大路长表示过工序A2的最大路长，则有T3≤T总。

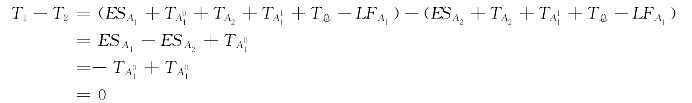
所以T1=T2。

所以②、③中路线的最大路长为ESA1+TA1+TA2+T总-LFA1。

调整后网络的最大路长为max{T总，ESA1+TA1+TA2+T总-LFA1}，A1是ES最小且LF最大的工序。

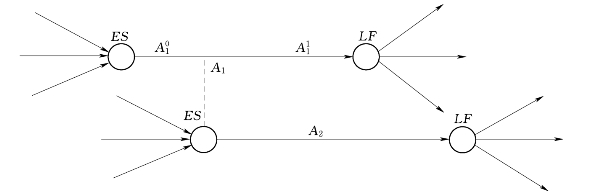
2）ESA1≤ESA2，LFA1＜LFA2，如图6-2所示。

(www.xing528.com)

图6-2　ESA1≤ESA2，LFA1＜LFA2

根据上面陈述，调整方式为→→，过调整后网络有两类路线：

①原有路线；

②过→→A2的路线。

在这2条路线中，②中路线的最大路长为ESA1+TA1+TA2-LFA2+T总，其中A1是最早开始最小工序，A2最迟结束时间最大工序。

所以调整后网络的最大路长为max{T总，ESA1+TA1+TA2-LFA2+T总}。

3）ESA1≤ESA2，LFA1=LFA2，如图6-3所示。

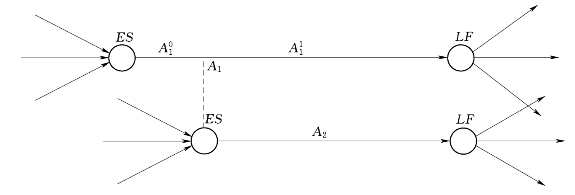
图6-3　ESA1≤ESA2，LFA1=LFA2

根据上面陈述，调整方式为→A2→或→→A2，同1），2）的分析，调整后网络的最大路长为

max{T总，ESA1+TA1+TA2-LFA1（LFA2）+T总}

综上所述，由1）、2）、3）可知，调整后网络新增路线的最大路长为max{T总，ESAi+TA1+TA2-LFAj+T总}，其中Ai表示最早开始时间最小工序，Aj表示最迟结束时间最大工序。

在优化方法分析的基础上，本书将给出亏值模型的建立和理论上的证明。

6.1.2.2　最小亏值模型的建立

亏值模型指若两个可分解平行工序A1，A2调整为顺序工序，最小亏值为max{T总，ESAi+TA1+TA2-LFAj，0}，其中Ai表示A1，A2最早开始时间最小工序，Aj表示A1，A2最迟结束时间最大工序（Ai和Aj可为同一工序）。

证明过程如下。

（1）由最小路长定理，将两个可分解平行工序A1，A2调整为顺序工序，有无数种调整方式。每种调整方式都有经过所有工序的最大路长，这些最大路长的最小值为ESAi+TA1+TA2-LFAj+T总，其中Ai表示A1，A2最早开始时间最小工序，Aj表示A1，A2最迟结束时间最大工序（Ai和Aj可为同一工序）。

（2）若把两个平行工序A1，A2任意分解后，不妨设A1可分解为，，…，；A2可以分解为，，…，，并组成顺序工序组：→→→…→，→→…→，→→…→，…

从组成的所有顺序工序组中任取一个→→…→，下面看网络调整后新增加路线。

1）必有过→→…→的路线，过该路线的最大路长为ESA1+TA1+TA2-LFA1+T总。

2）其他新增路线。

由已知Ai表示A1，A2最早开始时间最小工序，则有ESAi≤ESA1；Aj表示A1，A2最迟结束最大工序，则有LFAj≥LFA1。若把所有新增路线的最大路长记为，则有

（3）对任意两个可分解的平行工序A1，A2，总可以找到个调整方式，调整后网络的最大路长为max{ESAi+TA1+TA2-LFAj+T总，T总}。

（4）综合（1）、（2）、（3），两个可分解平行工序A1，A2调整为顺序工序，最小亏值为

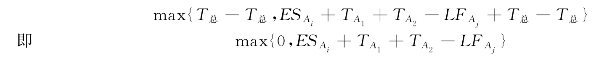
在已给亏值模型的基础上，将给出以下问题的优化算法。