案例分析：流程网络图与子网络工序机动时间

本节将对一个双层网络的机动时间进行分析，此网络来源于一个真实的案例。图5-7所示为此流程的总网络图G，图5-8和图5-9分别为总网络图G的第一层子网络S1 和第二层子网络S2。图中在箭线部分已经标出每个工序的持续时间。下面我们应用上节提出的分层网络机动时间计算方法对此网络的各时差进行分析，并在此基础上寻找此网络图的关键路线。

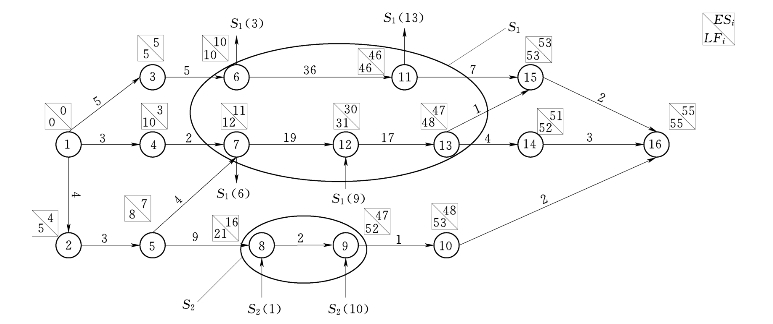
图5-7　总网络图G

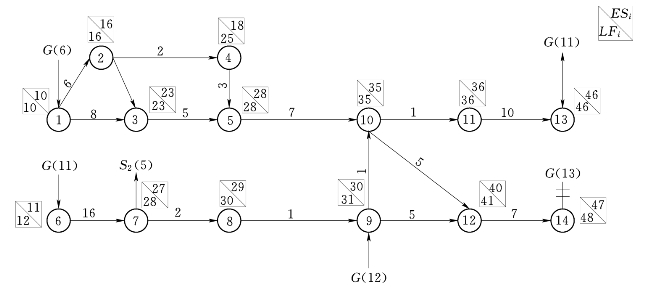
图5-8　子网络图S1

（1）时间参数的确定。从总网络G开始，令ESG（0）=0，按照公式ESGij={ESGhi+Thi}计算工序（1，2）、（1，3）、（1，4）、（2，5）、（3，6）、（4，7）、（5，7）和（5，8）的最早开始时间，由于总网络节点6和节点7是与子网络S1交汇处的节点，转入子网络S1继续计算，同理节点8为子网络S2与总网络的交汇点，转入子网络S2进行计算。通过时间参数的计算方法得到所有节点的最早开始时间和最迟结束时间，并标于网络图的节点上方，如图5-7、图5-8和图5-9所示。

（2）机动时间计算。根据求得的时间参数计算总网络G各工序机动时间（表5-1）。而对于子网络S1和子网络S2的机动时间计算需要考虑工序的紧前工序和紧后工序是否为上一层网络的交汇处，从而判断机动时间是否受到了外来网络的影响。例如，对于子网络S1的节点1，由于其与总网络G的节点6相交汇，而节点6在总网络中为关键节点，因此对于子网络的工序（1，2）的总时差有=TF12，其安全时差=SF12-SF1=10-10=0。由于其紧后工序不是与上一层网络的交汇处，所以其自由时差=FF12=-FF12=16-16=0。通过逐层计算得到子网络S1和子网络S2的各工序机动时间如表5-2和表5-3所示。

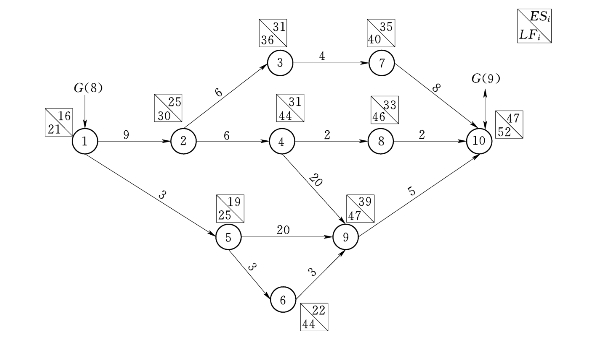
图5-9　子网络图S2

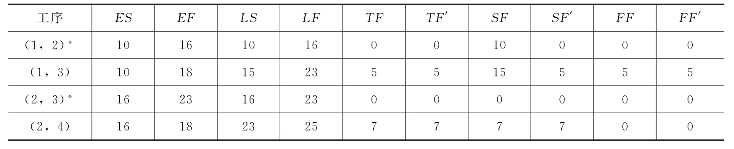
表5-1　总网络图G各工序机动时间

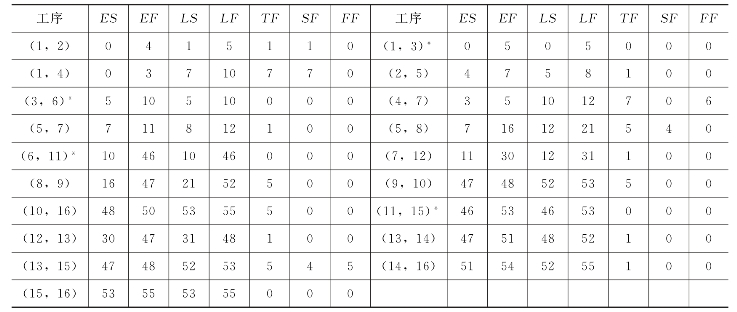(www.xing528.com)

*　表示关键工序。

表5-2　子网络S1各工序机动时间

续表

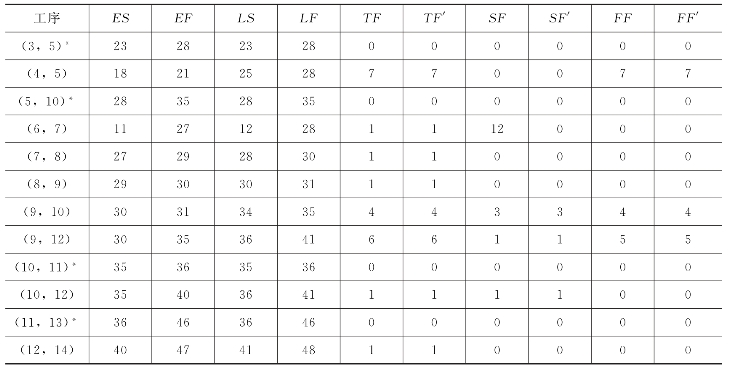
*　表示关键工序。

表5-3　子网络S2各工序机动时间

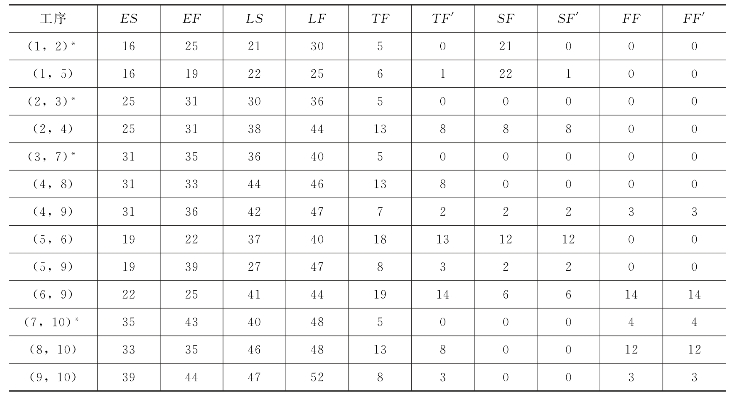
*　表示关键工序。

通过时间参数的逐层计算，底层网络均能知道各工序什么时候可以开始，必须在什么时候结束，可以灵活把握的时间到底有多少，从而更好地安排工作。

从上述的案例可知，通过分层网络技术，原本的大型项目网络图可以用多层次的小型的网络图表示出来，各层次的决策者也只需要把握好相关层次的进度控制，而不需要对网络做全面的了解，从而将精力集中到相关层次的决策当中，这对合理地进行资源分配和项目的集中管理具有重要意义。