案例分析：网络图优化和时间调整探讨

根据某项目的流程，画出其网络图（图4-1），粗箭线表示关键工序，箭杆上△内标注的数字是该工作每天所需资源数（假设所有工作都需要同一类资源）。现在资源有限，每日可用资源数为10，调整项目的进度计划，且尽量不延迟总工期或少延迟。

图4-1　某项目网络图

由图4-1可知，该网络图中无虚入点和虚出点。

（1）第一步调整。

1）绘制早时标网络图，如图4-2所示。

图4-2　早时标网络图

2）确定第1步调整的时间区间。因每日可用资源数为P=10，所以不用考虑提供资源时间段对时间区间的影响；=2，d1不存在，F0=0，则F1=2，时间区间为[0，2]。

3）LS（1，2）=0，LS（1，4）=1，LS（1，6）=7，=0，r1=10，所以R（1，2）+R（1，4）=9＜r1，R（1，2）+R（1，4）+R（1，6）=18＞r1，从而（1，6）后移，后移量ΔT=2。

4）因为ΔT＜TF（1，6）=7，且（1，6）没有后继工序，所以（1，6）后移不影响其他工序。

（2）第二步调整。

1）绘制第1步调整后的早时标网络图，如图4-3所示。

图4-3　早时标网络图（第1步调整后）

2）确定第2步调整的时间区间，不存在，d2=1，则F2=3，时间区间为[2，3]。

3）LS（2，3）=2，LS（1，6）=7，=3，r2=7，（1，6）后移，后移量ΔT=1。

4）因为ΔT＜TF（1，6）=5，且（1，6）没有后继工序，所以工序（1，6）后移不影响其他工序。

（3）第3步调整。(www.xing528.com)

1）绘制第2步调整后的早时标网络图，如图4-4所示。

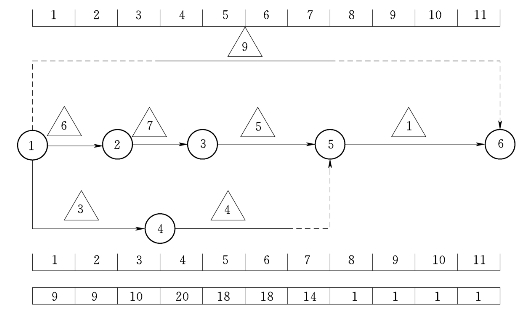
图4-4　早时标网络图（第2步调整后）

2）确定第3步调整的时间区间，=3，d3=1，则F3=4，时间区间为[3，4]。

3）LS（1，6）=7，LS（4，6）=8，=7，r3=3，（1，6），（4，6）后移，后移量ΔT=1。

4）因为ΔT＜TF（1，6）=4，ΔT＜TF（1，6）=5，且（1，6），（4，6）没有后继工序，所以（1，6），（4，6）后移不影响其他工序。

（4）第4步调整。

1）绘制第3步调整后的早时标网络图，如图4-5所示。

图4-5　早时标网络图（第3步调整后）

2）确定第4步调整的时间区间，=3，d4不存在，则F4=7，时间区间为[4，7]。

3）S（3，5）=4，LS（1，6）=7，LS（4，6）=8，R*4=0，r4=10，（1，6）后移，后移量ΔT=3。

4）因为ΔT＜TF（1，6）=3，且（1，6）没有后继工序，所以工序（1，6）后移不影响其他工序。

（5）第5步调整。

1）绘制第4步调整后的早时标网络图，如图4-6所示。

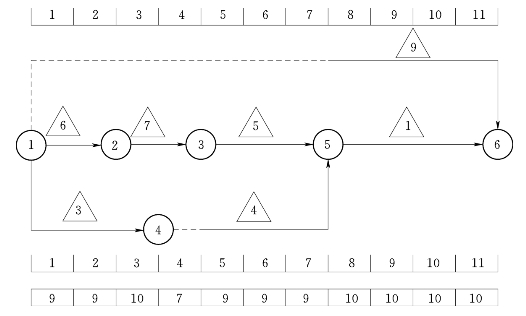
图4-6　早时标网络图（第4步调整后）

2）确定第5步调整的时间区间，=4，d5不存在，则F5=11，时间区间为[7，11]。

3）LS（1，6）=LS（5，6）=7，=0，r5=10，（1，6），（5，6）都不后移，调整结束。最后调整的时标网络图为图4-6。