相邻工序机动时间的关系

总时差、前共用时差、前单时差、后共用时差、后单时差，这么多种时差都反映了工序机动时间的性质，那么相邻工序的机动时间之间会有什么样的关系？我们将以相邻工序（k，i）和（i，j）为例，通过图2-1给出两者机动时间之间的关系。

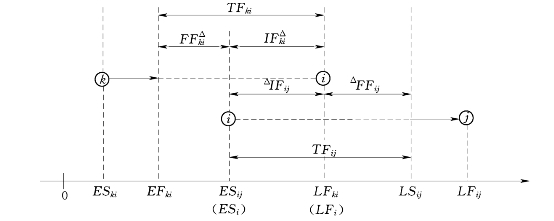
图2-1　总时差、前共用时差、前单时差、后共用时差、后单时差之间的关系

由图2-1可以看出：

（1）工序（i，j）使用自身前单时差和前共用时差的方式是它的开始时间从最迟开始时间起提前，并且先使用前单时差ΔFFij，后使用前共用时差ΔIFij。

（2）工序（k，i）使用自身后单时差和后共用时差的方式是它的结束时间从最早结束时间起推迟，并且先使用后单时差，后使用后共用时差。

（3）节点（i）的时差TFi既是紧前工序（k，i）的后共用时差，也是紧后工序（i，j）的前共用时差ΔIFij，即TFi==ΔIFij。从图2-1可以看出，这部分机动时间若工序（k，i）使用完，则工序（i，j）就不能再使用；若工序（k，i）不使用，则工序（i，j）可以使用，所以称其为共用时差。

在2.2节机动时间概念分析的基础上给出以下两个定理。

定理2.3　若EFij≥EFkmj，m=1，2，…，n，则=0，即共结束节点的工序中，最早结束时间最大的工序，其后单时差必定为零。

证明：由CPM网络中节点的时间参数计算方法可知(www.xing528.com)

ESj=max{EFk1j,EFk2j,…,EFknj,EFij}=EFij

其中，（k1，j），（k2，j），…，（kn，j），（i，j）表示节点（j）的紧前工序，所以

证毕。

定理2.4　若LSij≤LSirm，m=1，2，…，n，则ΔFFij=0，即共开始节点的工序中，最迟开始时间最小的工序，其前单时差必定为零。

证明：由CPM网络中节点的时间参数计算方法可知

LFi=min{LSij,LSir1,LSir2,…,LSirm}=LSij

其中（i，j），（i，r1），（i，r2），…，（i，rm）表示节点（i）的紧后工序，所以

ΔFFij=LSij-LFi=LSij-LSij=0

证毕。