在基本分析框架中优化第一价格密封拍卖的策略

对比上一节的英式拍卖，在第一价格密封拍卖中，竞标者不公开报出自己的竞价，而是以密封的形式将报价交给拍卖主持人，由主持人宣布报价最高者，即为版权拍卖的获胜者，并且以自己的密封报价支付给拍卖者来取得版权。于是，版权拍卖方在第一价格密封拍卖中的收益函数可以表示为：

类似的，要比较第一价格密封拍卖和英式拍卖中拍卖方取得的期望收益，首先需要确定竞标者的均衡投标策略，当竞标者以自己的估价作为密封报价，他能够获得的利润为0，因此竞标者同样以估价为限进行投标，竞标者1的利润函数直接可以得到：

Pr（wins）依然表示竞标者1获胜的概率，由于假设中关于竞标者是对称的，因此竞标者1和竞标者2的均衡策略不作区分，竞标者1的支付价格为b（v1）＝x，进一步计算有：

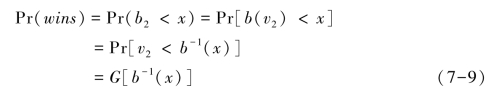
其中，b-1（x）是b（x）的反函数，b-1（b2）＝v2，竞标者1获胜的概率设为G（v1），将式7-9代入竞标者1的利润函数中得到：

竞标者的出价均是为了自身收益最大化的目的，对式7-10求一阶导数：

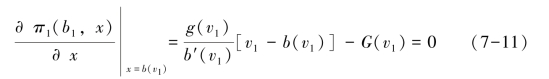
g（v1）为G（v1）的导数，由利润函数取得最大值的必要条件，令一阶导数等于0并移项转换得到：

这个就是竞标者1的均衡竞价策略，与英式拍卖相比，竞标者1在第一价格密封拍卖中的这一均衡策略显然不等于自己的真实估价。我们知道，在英式拍卖中，若竞标者1获胜，则他需要支付的价格为竞标者2退出拍卖时的报价，由于他们各自以自己的真实估价竞价，因此，竞标者1需要支付的价格为竞标者2的估价v2，获胜条件为v2＜v1，竞标者1此时支付价格的条件期望为：

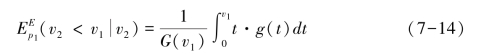
式7-14也可以看作是竞标者1获胜条件下竞标者2估价的分布值，而式7-13得到的结果恰好与式7-14相同，表明第一价格密封拍卖中竞标者1的均衡竞价策略并非以自己的真实估价出价，而是以自己获胜为前提，依据了解到的竞标者2估价的平均分布值作为投标策略。这一行为可以理解为：在第一价格密封拍卖中，竞标者的竞价越高，相应的胜出概率也会越大，但与此同时利润也会降低；想要增加利润，则必须降低自己的密封报价，则相应的获胜概率也会降低。如果竞标者采取类似英式拍卖的方式，使用自己的真实估价作为报价，那么所获利润就为零，因此竞标者选择的竞价策略必定会低于自己的真实估价，像式7-13的结果那样，竞标者1根据自己在拍卖中所能得到的私人信息来预估竞标者2的估价，将v2的条件期望值作为投标策略，条件为v2＜v1。

根据以上分析过程可知，由于第一价格密封拍卖中每个竞标者均使用相同的竞价策略，以竞标者2为例，当他知道竞标者1将采用平均股价作为竞价策略后，为了确保自己的胜利，他将刻意隐瞒部分信息使得自身估价表面看起来不高。因此，每个竞标者均会依据自身对其他竞争者的估价预测来出价，而竞价策略的出发点就是在取得拍卖胜利的同时，保证自身能够获取一定的利润，于是每个竞标者都会在一定程度上掩饰自身的真实估价，从而提高自身的获胜概率。因此第一价格密封拍卖中最终取得的均衡结果，取决于每个竞标者对自己真实估价所包含私人信息的遮蔽程度，这也是决定哪个竞标者会最终获胜的关键所在。

由于v1、v2服从区间上的均匀分布，那么可以知道英式拍卖中在满足获胜条件v2＜v1的情况下，竞标者1的支付价格为那么根据式7-13和式7-14的结果，可以得到在第一价格密封拍卖模型中，竞标者1的均衡竞价策略的解为：

综合上文分析可知，竞标者1在第一价格密封拍卖中的出价远低于自己的真实估价，遮蔽程度达到50%。本节得到的结果是由两个对称竞标者的平均估价分布计算得到的，只是为了说明竞标者在第一价格密封拍卖中如何得到自身的竞价策略，且他们的出价都会在一定程度上选择遮蔽自己的真实估价。

为了证明上文得到的式7-13是竞标者1在第一价格密封拍卖中的最优竞价策略，我们现在假设竞标者1最终的出价为x˜而不是x，且有b（y）＝x˜，得到竞标者1的利润函数为：

(www.xing528.com)

将式7-13的结果代入，并且将积分进行分部转化，进一步计算得到：

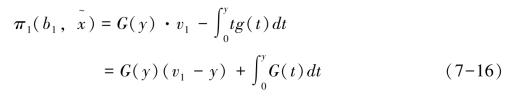
竞标者1的最终竞价若为＝b（y），则y存在两种情况，一种是y＜v1，另一种是y＞v1，我们还是像英式拍卖中使用图形来证明竞标者1的最优策略如何确定，图7-2（a）中为第一种情况y＜v1，图7-2（b）为第二种情况y＞v1。

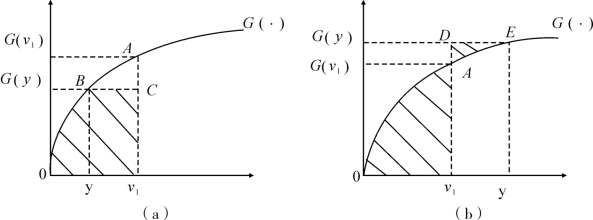
图7-2　利润函数

注：（a）y＞v1；（b）y＜v1

如图7-2所示，在第一种情况中，竞标者1的利润函数可以用图形中的阴影部分的面积来表示，由式7-16的表达式可知，利润函数为图形0By和BCv1y的面积之和，若投标者将出价从b（y）提高到b（v1），则他可以获得增加的利润ABC的面积，此时提高出价是有利的；与此同时，在图7-2（b）的情况下，投标者1获得的利润为图形0v1A与ADE的面积之差，此时若竞标者将出价由b（y）逐渐降低到b（v1），可以增加面积为ADE的那一部分利润，这对竞标者来说同样是有利可图的。由于竞标者都是理性经济人，他们的竞标策略都是为了使自己的期望收益最大化，因此在第一价格密封拍卖假设的基本模型推论中，竞标者1最终选择的竞标策略为x＝b（v1）＝

由此，竞标者1的竞价策略得到的结果为式7-15中那样，有其假设条件是竞标者2的估价小于竞标者1的估价，即v2＜v1则会有b（v2）＜b（v1），表示在第一价格密封拍卖中，估价较高的竞标者将会赢得拍卖，同英式拍卖中得到的结论一样，拍卖者总是能将拍卖标的以较高的价格转让出去，从而获得较高的收益，说明第一价格密封拍卖的均衡竞价结果也是有效率的。

确定了竞标者的均衡竞价策略，可以计算出拍卖者获得的期望收益，根据之前的推导可知，当竞标者1在拍卖中获胜的时候，即v2＜v1，他需要支付的期望价格为：

由第二节中的模型基本假设，拍卖中存在的两个投资者对称，那么当竞标者2获胜的时候，他的期望支付与竞标者1相等，由此可以推导出拍卖者可以获得的期望收益：

从式7-18可以看出，这一结果与英式拍卖中拍卖者得到的期望收益并没有不同，都是在一方获胜的条件概率下发生的获胜竞标者的期望支付的总和。要进一步确认这个结果，我们用另一种方法进行具体的计算过程：

将式7-15的均衡竞价策略的结果代入式7-8中，则拍卖者的期望收益公式变成：

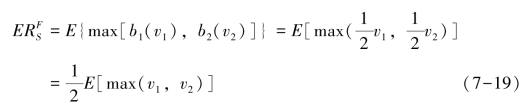
同样地，设λ＝max（v1，v2），由于v1，v2相互独立，且服从区间[0，]上的均匀分布，则λ的分布函数和密度函数分别为：

进一步地，拍卖者的期望收益可以得到：

以上结果验证了关于式7-18的说法，即拍卖者在英式拍卖和第一价格密封拍卖中所能获得的期望收益是相同的，尽管在第一价格密封拍卖中竞标者的均衡出价策略为，相比英式拍卖中的均衡策略bE（v）＝v更低，竞标者根据自己的投标价格进行实际支付，因此均会选择遮蔽自己的真实估价，但是拍卖者最终所能获得的期望收益却并未受到影响，这也证明了等价收益定理，即版权拍卖方能够在英式拍卖和第一价格密封拍卖中获得的期望收益是相等的。

对于这一结论可做如下解释：在英式拍卖中，每个竞标者都根据自己的真实估价出价，拍卖者却无法得知每个竞标者的出价，因此在这种方式下价格竞争是在所有参与者均知晓的情况下进行，最高估价竞标者能够随时根据竞价情况来决定是否退出拍卖。在信息不对称的情况下，竞标者能够根据自身对实际估价信息的了解程度来获得超额收益，英式拍卖的性质也决定了最高估价竞标者的最终支付金额为最后退出拍卖竞标者的报价，因此这部分信息租金将归最终获胜的竞标者所有。第一价格密封拍卖的实质为拍卖者对版权实行价格歧视销售，虽然竞标者会遮蔽自己的真实估价，但最终也是由最高出价竞标者获得所拍卖的版权，从而收获一部分消费者剩余作为补偿。综合以上信息租金和价格歧视两种因素来看，只要版权投资者的估计符合相互对称的独立私人假设，那么无论是在第一价格密封拍卖定价机制中还是在英式拍卖定价机制中，拍卖者所获得的期望收益都是相同的。