从观察一些特殊的简单的问题入手,根据它们所体现的共同性质,运用不完全归纳法作出一般命题的猜想,由于这个猜想是通过试验、观察、分析、综合、抽象概括出来的,其缺点是探索得到的猜想不一定正确,需要加以证明,而数学归纳法只能对所发现的结论正确与否加以论证,不能直接发现结论,因此,将不完全归纳法与数学归纳法并举是一种探讨数学问题的好方法,从而就有了“归纳—猜想—证明”题型,它是一个完整的思维过程,是人们从事科学研究,认识发现规律的有效途径,归纳是“猜想”的前提,它体现了由“特殊”到“一般”的转化,为了增强“猜想”结论的可靠性,在“归纳”阶段,一般应多演算几种特殊情形,然后通过对特殊的情形的分析去研究其一般规律,最后结论的正确性必须用数学归纳法证明.当然,有些题也可以由特殊到一般进行分析论证.
例1 (1)观察下表:
1=1
3+5=8
7+9+11=27
13+15+17+19=64
21+23+25+27+29=125
…
推测由上表各行所提示的一般规律,用适当的数学记号表达并加以证明.
(2)观察下列各式:
①![]()
②![]()
③![]()
④![]()
…
根据以上信息,猜想一般规律,并加以证明.
解题策略 不完全归纳法是从对个别命题或特殊论断的探讨与分析中,猜测普遍命题或一般结论的方法,猜测所得的结论可能正确也可能不正确,需要加以证明,可以运用数学归纳法证明(与自然数n相关的命题),也可以利用合情推理作出猜想,用演绎推理进行证明.本例两小题侧重于讨论发现过程,运用演绎推理证明,第(1)问,观察给出的一系列等式,不难发现右边为n3(n为第n个等式),左边是公差为2的等差数列之和,解题关键是探究出其首项与n的关系,得出猜想,然后证明.第(2)问,猜想结果并不困难,应用归纳推理需要进行三角恒等变形,并按奇偶分类证明.
解:(1)由观察可知,各等式右侧的数依次为13,23,33,43,53,…,可猜测第n行等式右侧的数为n3.
对于左侧,第n行应是n个奇数之和,各行的第一个奇数依次为1,3,7,13,21,…,进一步可写成0+1,2+1,6+1,12+1,20+1,…,即0×1+1,1×2+1,2×3+1,3×4+1,4×5+1,…
故可猜想第n行左侧第一个奇数为(n-1)n+1,进而后续奇数依次为(n-1)n+3,(n-1)n+5,…,(n-1)n+(2n-1),
于是第n行等式可猜想为:
[(n-1)n+1]+[(n-1)n+3]+[(n-1)n+5]+…+[(n-1)n+(2n-1)]=n3.
即(n2-n+1)+(n2-n+3)+…+(n2+n-1)=n3.
该等式的证明如下:
左边![]() 右边.
右边.
(2)根据题目给出的信息,猜想一般规律为:
![]()
证明 由二倍角正弦公式![]()
据此可得![]()

当n为偶数时,则有
原式
注意到以下这些角互补,即
![]()
![]()
同理可得当n为奇数时结论亦成立.
例2 已知函数y=f(x)与函数![]() 的图像关于直线y=x对称.
的图像关于直线y=x对称.
(1)在数列{an}中,a1=1,当n≥2时,an>a1,在数列{bn}中,b1=2,Sn=b1+b2+…+bn,若点![]() 在函数f(x)的图像上,求a的值;
在函数f(x)的图像上,求a的值;
(2)在(1)的条件下,过点Pn作倾斜角为![]() 的直线ln,ln在y轴上的截距为
的直线ln,ln在y轴上的截距为![]() 求数列{an}的通项公式.
求数列{an}的通项公式.
解题策略 本例是一道以数列为载体的能力题,结合函数与解析几何的一些知识,其解题核心是“观察、猜测、抽象、概括、证明”,这是发现问题和解决问题的重要途径.实际上,数学中的难点一般都是在观察归纳、猜测证明的过程中得以突破的.
解:(1)因为函数f(x)是![]() 的反函数,所以
的反函数,所以![]()
因为点![]() 在函数f(x)的图像上,所以
在函数f(x)的图像上,所以![]() ①
①
令n=1,得![]() 则a=1.
则a=1.
(2)由(1)得a=1,①式可化为![]() ②
②
直线ln的方程为:![]()
因为ln在y轴上截距为![]() 所以
所以![]()
结合②式可得![]() ③
③
由②式可知,当自然数n≥2时,![]()
两式作差得![]() 结合③式得
结合③式得
![]() ④
④
在④式中,令n=2,结合a1=1,可解得a2=1或2,
又因为当n≥2时,an>a1,所以a2=2.
同理,在④式中,依次令n=3,n=4,可解得a3=3,a4=4.
由此猜想an=n,然后用数学归纳法证明如下:
❶当n=1,2,3时,已证成立;
❷假设当n=k时命题成立,即ak=k(k∈N*,且k≥3),
当n=k+1时,由④式可得![]()
把ak=k代入,解得![]() 或k+1.
或k+1.
由于k≥3,则![]() 所以
所以![]() 不符合题意,应舍去,故只有ak+1=k+1,则当n=k+1时命题也成立.
不符合题意,应舍去,故只有ak+1=k+1,则当n=k+1时命题也成立.
综上可知,数列{an}的通项公式为an=n.
例3 已知数列{an},{bn}分别满足![]()
(1)求a2,a3,猜想并证明{an}的通项公式;(https://www.xing528.com)
(2)若![]() 证明:c1c2…cn<2·n!
证明:c1c2…cn<2·n!
解题策略 解决“归纳—猜想—证明”类问题以及不等式的证明时,容易有以下几点误区.
(1)在运用不完全归纳法猜想时,由于归纳整理不到位或中间某环节出现运算错误,从而给猜想造成困难.
(2)证明n=k到n=k+1这一步时,忽略了假设条件去证明,造成不是“纯正”的数学归纳法或者可以说是完全归纳法过程中有缺失.
(3)不等式证明过程中,不能正确合理地运用分析法、综合法来求证,或者当直接用数学归纳法证明不等式有困难时,不会通过先证明加强不等式(可能找不到)来达到证明原不等式的目的.
解:(1)由![]() 得
得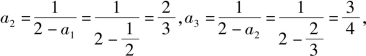
猜想![]() 下面用数学归纳法证明:
下面用数学归纳法证明:
❶当n=1时,左边![]() 右边
右边![]() 猜想成立;
猜想成立;
❷假设当n=k时猜想成立,即![]()
则当n=k+1时, 故当n=k+1时,猜想也成立.
故当n=k+1时,猜想也成立.
由❶❷,可得对![]() 成立.
成立.
(2)由![]() 知,
知,![]()
所以![]() 即
即![]()
而![]() 所以
所以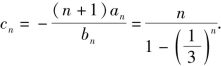
故欲证c1c2…cn<2·n!,等价于证明 即证明
即证明![]()
证法一 当n=1时,不等式显然成立;当n≥2时,先证明加强不等式:
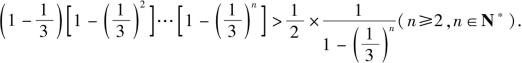
❶当n=2时,左边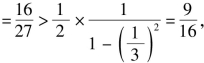 即不等式成立;
即不等式成立;
❷假设n=k时不等式成立,即
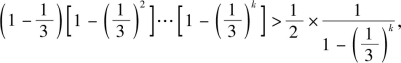
则当n=k+1时,
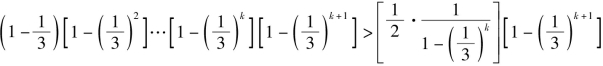
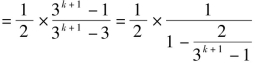 ①
①
因为![]() 所以
所以![]() 从而有
从而有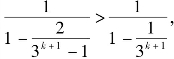 所以①式
所以①式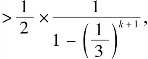 故当n=k+1时,结论成立.
故当n=k+1时,结论成立.
由上及数学归纳法可得,n≥2时,
故有![]() 所以得证.
所以得证.
证法二 先证明加强不等式![]()
❶当n=1时,左边![]() 不等式成立;
不等式成立;
❷假设n=k时不等式成立,即![]() 则当n=k+1时,
则当n=k+1时,
![]()
![]() 故当n=k+1时,结论成立.
故当n=k+1时,结论成立.
由数学归纳法可得,![]() 故有
故有![]() 所以得证.
所以得证.
例4 如图12-3所示,已知动圆与直线y=-3相切,并与定圆x2+y2=1相内切.
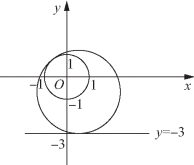
图12-3
(1)求动圆圆心P的轨迹C的方程;
(2)过原点作斜率为1的直线交曲线C于P1(P1为第一象限点),又过P1作斜率为![]() 的直线交曲线C于P2,再过P2作斜率为
的直线交曲线C于P2,再过P2作斜率为![]() 的直线交曲线C于P3,……,如此继续,过Pn作斜率为
的直线交曲线C于P3,……,如此继续,过Pn作斜率为![]() 的直线交曲线C于Pn+1,设Pn(xn,yn).
的直线交曲线C于Pn+1,设Pn(xn,yn).
❶令bn=x2n+1-x2n-1,求证:数列{bn}是等比数列;
❷数列{bn}的前n项和为Sn,试比较![]() 与
与![]() 的大小.
的大小.
解题策略 本例以解析几何为载体,重点突出数学归纳法的应用,感知“观察→归纳→猜想→证明”的思考与解决的过程,体验其中所呈现的数学之美.
解:(1)由题意知,点P到原点的距离等于点P到直线y=-2的距离,由抛物线定义知,点P轨迹是以原点为焦点,直线y=-2为准线的抛物线,其轨迹方程为x2=4(y+1).
(2)❶设Pn(xn,yn),Pn+1(xn+1,yn+1),则![]()
因为直线PnPn+1的斜率为![]() 有
有![]()
所以![]() 即
即![]()
所以bn=x2n+1-x2n-1
=(x2n+1+x2n)-(x2n+x2n-1)
![]()
![]()
![]()
所以数列{bn}是以-1为首项,![]() 为公比的等比数列.
为公比的等比数列.
❷由 ❶知![]() 所以
所以![]()
所以![]() 下面只要比较4n与3n+10的大小;
下面只要比较4n与3n+10的大小;
当n=1时,4<13,有4n<3n+10;当n=2时,16=16,有4n=3n+10;
当n=3时,64>19,有4n>3n+10;猜测当n≥3,n∈N时,4n>3n+10.
证法一 用数学归纳法证明,当n≥3,n∈N时,4n>3n+10.
(i)当n=3时,已成立;
(ii)假设当n=k(k>3,n∈N)时,4k>3k+10.
则当n=k+1时,4k+1=4·4k>4(3k+10)=[3(k+10)+10]+9k>3(k+1)+10,
即当n=k+1时,4n>3n+10也成立.
由(i)(ii)知,当n≥3,n∈N时,4n>3n+10都成立.
证法二 利用二项式定理,得
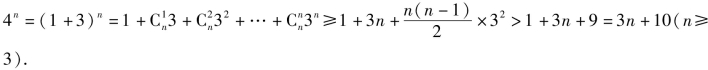
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




