数学的创造能力一般指对已经掌握的数学知识、方法进行推广和拓展,对未知的数学领域通过探索得到新的结果的能力,而类比法就是这种创造能力的一个方面、一种体现,通过类比可以由此及彼发现新问题,总结新规律,也可以对原有问题在知识层面或方法层面上加以拓展,使认识不断深入,并推广到更为一般的结论.
运用类比法的关键是寻找一个合适的类比对象,但是很多待解决的问题没有现成的类比物,这就需要我们通过观察、提炼,凭借结构上的相似性寻找类比对象,类比的基础是联想的发生,而联想的发生是以与问题相关的丰富的知识为基础的,高中阶段所学的基本上属于古典数学范畴,但是随着时代的进展,我们要改变对原有知识的认识方式.
例1 (1)函数f(x)对于任何x∈R+,恒有f(x1·x2)=f(x1)+f(x2),若f(16)=4,求f(4);
(2)定义在R+上的函数f(x)满足:①f(10)=1;②对任意实数b,f(xb)=bf(x).
❶求![]() 及满足f(k-1003)=lg1003的k值;
及满足f(k-1003)=lg1003的k值;
❷求证:对任意实数x,y<R+,f(xy)=f(x)+f(y);
❸求证:f(x)是R+上的增函数.
解题策略 第(1)问,从给出的抽象函数的条件着手进行类比,其形式正是对数函数具有的性质:loga(xy)=logax+logay(x,y∈R+);第(2)问,由条件易知本题的模型函数为f(x)=lgx,则各小题的求解或证明思路豁然开朗,完全可以借助函数f(x)=lgx的特有性质进行求解或证明.
解:(1)类比对数函数的性质,若设f(x)=log2x,则满足f(16)=log216=4,因此,f(4)=log24=2.
(2)❶由题意可知本题的模型函数为f(x)=lgx,
![]()
![]()
∵f(k-1003)=f[10lg(k-1003)]=lg(k-1003)·f(10)=lg(k-1003)=lg1003,
∴k-1003=1003,解得k=2006.
❷证明 设x>0,y>0,当x≠1时,
f(xy)=f(x·xlogxy)=(1+logxy)·f(x)=f(x)+logxy·f(x)=f(x)+f(xlogxy)
=f(x)+f(y),当x=1时,f(y)=f(1)+f(y),而f(1)=0,也适合,
故当x>0,y>0时,f(xy)=f(x)+f(y).
❸证明 当x>1时,f(x)=f(10lgx)=lgx·f(10)=lgx>0.
设0<x1<x2,则![]() 即
即![]()
由❷知![]()
∴f(x)是R+上的增函数.
例2 (1)若函数f(x)(x∈R)满足:f(x+m)=f(x+m)f(x)+1+f(x),且f(x)≠1,m是非零常数,问f(x)是否是周期函数?若是,求出它的一个周期,若不是,请说明理由.
(2)如图12-1所示,F1,F2是椭圆![]() 的两个焦点,P在椭圆上,若设∠F1PF2=θ,则△F1PF2的面积为
的两个焦点,P在椭圆上,若设∠F1PF2=θ,则△F1PF2的面积为![]() 相应地,如图12-2所示,F1,F2是双曲线
相应地,如图12-2所示,F1,F2是双曲线![]() 的两个焦点,P在双曲线上,若设∠F1PF2=θ,则△F1PF2的面积S的表达式是什么?并对两个命题加以证明.
的两个焦点,P在双曲线上,若设∠F1PF2=θ,则△F1PF2的面积S的表达式是什么?并对两个命题加以证明.
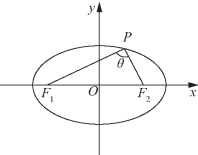
图12-1
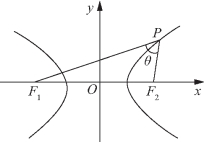
图12-2
解题策略 类比推广通常有两种基本题型,一种是由所给的问题或关系式类比联想它的背景或原型,找到一种清晰简捷的解法,此类题要求学生具备一定的数学基础,以及猜想能力与模仿能力,比如第(1)问;另一种是两种相近知识之间的类比推广,比如第(2)问,椭圆焦点三角形的面积公式已经给出,可通过解三角形以及三角恒等变形加以证明,而双曲线与椭圆之间有差异也有联系,关键是寻找出“似曾相识”的因素,类比迁移,借石攻玉.
解:(1)![]() 联想到三角公式
联想到三角公式![]()
不难得知其结构模型与![]() 类同,若视式中的m为
类同,若视式中的m为![]() 时,则可把tanx看成是f(x)的一个原型实例,而y=tanx是周期为T=π的周期函数且是
时,则可把tanx看成是f(x)的一个原型实例,而y=tanx是周期为T=π的周期函数且是![]() 的4倍,由此可类比猜测f(x)是周期为4m的周期函数.
的4倍,由此可类比猜测f(x)是周期为4m的周期函数.
事实上,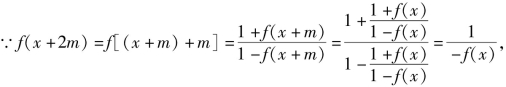
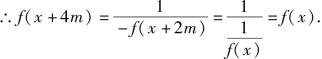
故f(x)是周期为4m的周期函数.
(2)对于双曲线![]() 相应的∠F1PF2的面积表达式是
相应的∠F1PF2的面积表达式是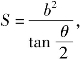 两个命题证明如下:
两个命题证明如下:
由椭圆的定义知|PF1|+|PF2|=2a,由![]() 得
得![]()
由余弦定理知![]() =
=![]() -2|PF1||PF2|cosθ
-2|PF1||PF2|cosθ
=(|PF1|+|PF2|)2-2|PF1||PF2|(1+cosθ),
即![]() 故
故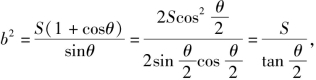
从而![]()
相应地,由双曲线的定义,|PF1|-|PF2|=±2a,
由![]() 得
得![]()
由余弦定理得![]() =
=![]() -2|PF1||PF2|cosθ(https://www.xing528.com)
-2|PF1||PF2|cosθ(https://www.xing528.com)
=(|PF1|-|PF2|)2+2|PF1||PF2|(1-cosθ),
即![]() 故
故
从而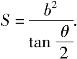
例3 设P1(x1,y1),P2(x2,y2)是函数![]() 图像上的两点,且
图像上的两点,且![]()
(1)若点P的横坐标为![]() 求证:P点的纵坐标为定值,并求出这个定值;
求证:P点的纵坐标为定值,并求出这个定值;
(2)若![]() 求Sn;
求Sn;
(3)记Tn为数列![]() 的前n项和,若
的前n项和,若![]() 对一切n∈N*都成立,试求a的取值范围.
对一切n∈N*都成立,试求a的取值范围.
解题策略 类比迁移的关键在于先弄清问题中给出的原命题的运算原理或结构,再在新的条件环境下类比出新命题,或依照高考命题的原则“源于课本,高于课本”,根据课本中介绍的数学方法推广出一些新的方法,如课本中用“逆序相加法”推导等差数列前n项和的方法可以迁移到本例第(1)问、第(2)问的解答中,第(3)问中需要运用“裂项相消法”,这也是课本中相关方法的类比推广.
解:(1)证明 由![]() 得P是P1P2的中点,从而x1+x2=1.
得P是P1P2的中点,从而x1+x2=1.
所以y1+y2![]()
![]()
由此得![]()
(2)由(1)知![]()
![]()
![]()
两式相加得2Sn=![]()
![]()
![]() 故
故![]()
(3)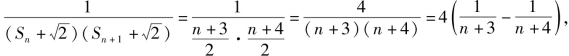
![]()
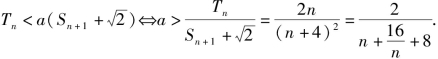
因为![]() 当且仅当n=4时,取“=”,所以
当且仅当n=4时,取“=”,所以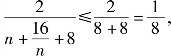 得
得![]()
例4 若椭圆![]() 和椭圆
和椭圆![]() 满足
满足![]() 则称这两个椭圆相似,m称为其相似比.
则称这两个椭圆相似,m称为其相似比.
(1)求经过点![]() 且与椭圆
且与椭圆![]() 相似的椭圆方程;
相似的椭圆方程;
(2)设过原点的一条射线l分别与(1)中的两个椭圆交于A,B两点(其中点A在线段OB上),求|OA||OB|的最大值和最小值;
(3)对于真命题“过原点的一条射线分别与相似比为2的两个椭圆![]() 和
和![]() 交于A,B两点,P为线段AB上的一点,若|OA|,|OP|,|OB|成等比数列,则点P的轨迹方程为
交于A,B两点,P为线段AB上的一点,若|OA|,|OP|,|OB|成等比数列,则点P的轨迹方程为![]() 请用类比法提出类似的一个真命题,并给予证明.
请用类比法提出类似的一个真命题,并给予证明.
解题策略 本题是一道新情景题,由比与比例以及两个相似三角形的相似比加以引申,给出椭圆相似比的概念,进而引出一个值得探究的问题,从而考查学生理解新概念的能力和掌握椭圆的标准方程、直线与圆锥曲线关系、弦长、最值等基础知识以及基本解题技能,引发学生提出新问题、解决新问题,从而更深入地考查学生对函数与方程思想、类比推广思想掌握的深度与广度,是一道具有挑战性、开放性特点,且有助于开展研究性学习的题目.
解:(1)设与椭圆![]() 相似的椭圆方程为
相似的椭圆方程为![]()
则有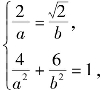 解得
解得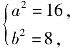 所以所求的椭圆方程为
所以所求的椭圆方程为![]()
(2)当射线与y轴重合时,![]()
当射线不与y轴重合时,由椭圆的对称性,我们仅考查A,B在第一象限的情形,设其方程为y=kx(k>0,x>0),设A(x1,y1),B(x2,y2).
由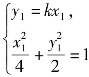 得
得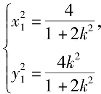 则
则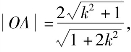 同理得
同理得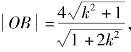
所以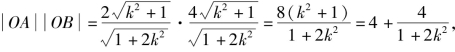
即4<|OA||OB|≤8.
综上所述,|OA||OB|的最大值为8,最小值为4.
(3)过原点的一条射线分别与两双曲线![]() 和
和![]() 交于A,B两点,P为线段AB上一点,若|OA|,|OP|,|OB|成等比数列,则点P的轨迹方程为
交于A,B两点,P为线段AB上一点,若|OA|,|OP|,|OB|成等比数列,则点P的轨迹方程为![]()
证明 因为射线l与双曲线有交点,不妨设其斜率为k,显然![]()
设射线l的方程为y=kx,点A(x1,y1),B(x2,y2),P(x,y).
由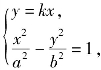 解得
解得![]()
由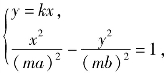 解得
解得![]()
由P点在射线l上,且![]() =|OA||OB|得
=|OA||OB|得 即
即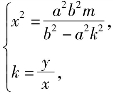
消去k即得点P的轨迹方程为![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




