简化与避免分类讨论的方法及实施

分类讨论思想解题的实质是“化整为零，各个击破，再积零为整”的思维策略，但有时，更应注意充分挖掘求解问题中潜在的特殊性和简单性，尽可能消除“讨论因素”，灵活地采用相应的解题策略，通过适当的“技术处理”，消化或避免分类讨论，往往能给解题带来事半功倍之效，避免分类讨论常见的解题策略有：直接回避、变更主元、整体考虑、反客为主、数形结合等.

例1　(1)解不等式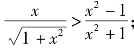

(2)设a∈R，函数f(x)=ax2+x-a(-1≤x≤1)，求当|a|≤1时，|f(x)|的取值范围.

解题策略　第(1)问，无理分式不等式按常规解法，必须分类讨论，通过三角换元，引进参数α，则无理不等式可以化为有理不等式，分式不等式也容易化为整式不等式，这是直接回避分类讨论的常用基本方法；第(2)问，绝对值问题常需分类，若能利用绝对值的性质整体考虑，也能直接回避分类讨论.

解：(1)设则原不等式可化为2sin2α-sinα-1<0，由此解得故从而原不等式的解集为

(2)

当且仅当及|a|=1时，

故|f(x)|的取值范围为

例2　(1)已知对于f(t)值域内的所有实数m,不等式x2+mx+4>2m+4x恒成立，则实数x的取值范围是________；

(2)已知函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]上至少存在一个实数c,使得f(c)>0,求实数p的取值范围.

解题策略　第(1)问，若按常规思路，将x看成主元，则要分很多情况来讨论m,无形之中增加了解题负担.若将m看成主元，则原不等式转化为一次不等式恒成立问题，易解.可见变换主元、反客为主可以有效避免分类讨论.第(2)问，若采取正面直接求解，由于二次函数的对称轴在变动，需要分多种情况考虑，而如果考虑对立面，情况就变得简单，这就是正难则反思想，可以有效避免讨论，结合图形看，非常直观.

解：(1)原问题转化为m(x-2)+(x-2)2>0对任意的恒成立.

当x=2时，不等式不成立，∴x≠2.

令即把g(m)看作关于m的一次函数.

问题转化为g(m)在上恒大于0，则解得x>2或x<-1.

即实数x的取值范围为(-∞，-1)∪(2，+∞).

(2)至少存在一个实数c，使得f(c)>0，需要分多种情况考虑，而考虑反面的话，即对于区间[-1，1]上任意的实数c都有f(c)≤0，结合图形可知，只需要满足f(-1)≤0且f(1)≤0即可，解得

取补集可得所求范围为

例3　(1)设偶函数f(x)定义在[-2，2]上，且在区间[0，2]上递减，若f(1-m)<f(m)，求实数m的取值范围.

(2)已知函数f(x)=-2x2+4x-1(x∈R)，定义域为[m，n]，且m>0，值域为求m，n的值.

解题策略　第(1)问，通常需要分4种情况讨论求解，要避开这场“大规模”的分类讨论，必须注意对隐含条件的挖掘.把握偶函数满足f(x)=f(-x)=f(|x|)这一本质，整体考虑，则问题即刻变得非常简单.第(2)问，若一个数学问题的题设中还含有一些隐含条件，如果稍加留意，充分挖掘，就能避免复杂的分类讨论，从而简化解答过程，挖掘求解问题中潜在的特殊性和简单性，尽可能消除“讨论因素”，回避分类讨论.在本题中若没有注意到隐含条件，不在大处着眼，很容易想到分3种情况讨论区间[m,n]与对称轴直线x=1的位置关系，而实际上，区间[m,n]在对称轴x=1的右边是可确定的，所以深挖隐含条件可避免讨论.

解：(1)∵f(x)为偶函数，∴f(1-m)<f(m)等价于f(|1-m|)<f(|m|).(www.xing528.com)

又f(x)在[0，2]上递减，∴2≥|1-m|>|m|，

由此解得m的取值范围为

(2)f(x)=-2x2+4x-1=-2(x-1)2+1≤1,因此区间必定包含在即m≥1，因此区间[m,n]为函数的减区间，

且

∴m，n是方程即(x-1)(2x2-2x-1)=0的两个解，

解得

∵1≤m<n,

例4　已知一条曲线C在y轴右边，C上每一点到点F(1，0)的距离减去它到y轴距离的差是1.

(1)求曲线C的方程；

(2)是否存在正数m，对于过点M(m,0)且与曲线C有两个交点A，B的任一直线，都有？若存在，求出m的取值范围；若不存在，请说明理由.

解题策略　当直线过一定点，很容易想到直线方程为点斜式或斜截式，从而忽略斜率不存在的情况，若从题设中可以判定直线的斜率不可能为零时，则可将直线方程设为x=ty+m，这样，不仅避免或简化了讨论的步骤，还可以大大减少计算量，从而提高解题速度，也可以说这是一种整体考虑的解题策略，直线方程x=ty+m中包含了斜率存在与不存在的情况.

解：(1)由题意知C上每一点到点F(1，0)的距离等于到直线x=-1的距离，根据抛物线的定义，可得曲线C的方程为y2=4x.

(2)显然，过点M的直线存在垂直于x轴的情况，但又不含垂直于y轴的情况，因此为了避免分类，可设直线方程为x=ty+m，并设A，B两点的坐标分别为(x1,y1)，(x2,y2).

将直线方程x=ty+m与抛物线方程y2=4x联立，

消去x得y2-4ty-4m=0.

Δ=16t2+16m>0恒成立(正数m)，y1+y2=4t，y1y2=-4m，

由得x1x2-(x1+x2)+1+y1y2<0，

∴m2-4t2-2m+1-4m<0，即m2-6m+1<4t2.

∵对任一直线，都有故m2-6m+1<4t2在t∈R上恒成立.

∴m2-6m+1<0，解得

可见，存在正数m，对于过点M(m,0)且与曲线C有两个交点A，B的任一直线，都有的取值范围为