使用分类讨论法解决立体几何问题：优化技巧分享

在研究空间直线与直线、直线与平面、平面与平面位置关系时往往会出现不同的状况需要分类讨论，在进行空间图形中有关面积和体积计算时，由于某一元素的变动而出现多种结果，也需要运用分类与整合的方法求解.

例1　已知直线AB∥CD且相距28cm，EF在AB，CD所确定的平面α外，EF∥AB且相距17cm，EF和平面α相距15cm，求EF与CD间的距离.

解题策略　本例是由于图形的位置关系不确定而引起分类讨论的立体几何问题，EF在平面α上的射影位置不同，则EF与CD的距离也不同，对各种情形都要讨论，否则就容易漏解或无从下手.

解：在EF上任取一点M，作MO⊥α于O，则垂足O的位置有两种可能：

❶在平行直线AB与CD之间，如图11-10(a)所示；

❷不在平行直线AB与CD之间，如图11-10(b)和图11-10(c)所示.

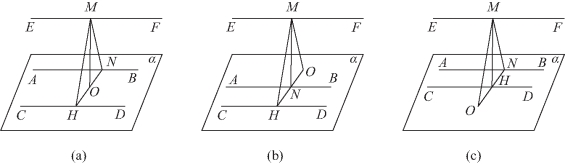
图11-10

在平面α内，过O作与AB，CD垂直的直线交CD于H，交AB于N，则MO=15cm为EF与平面α的距离，MN=17cm为EF与AB的距离.NH=28cm为平行直线AB，CD间的距离，MH为EF，CD间的距离.无论哪种情形，都有

在图11-10(a)中，OH=NH-ON=20cm，

在图11-10(b)中，OH=ON+NH=36cm，

在图11-10(c)中，OH=ON-NH=-20cm，此情况不存在.

因此EF与CD间的距离为25cm或39cm.

例2　若一个三棱锥的三个侧面中有两个是等腰直角三角形，另一个是边长为1的正三角形，试求所有满足上述条件的三棱锥的体积.

解题策略　三棱锥的三个侧面中只有一个面的形状是完全确定的，即是边长为1的正三角形，另有两个侧面是等腰三角形，实质上形状没有完全确定，构成三棱锥第四个三角形的形状有多种可能性，如图11-11所示，可以是与两个等腰三角形全等，也可以与边长为1的正三角形全等，若两个侧面是全等的等腰直角三角形，则第四个面是以等腰直角三角形的底边为腰、边长1为底的等腰三角形，所以解答本题的关键是构造符合题意的三棱锥，获得完整的解答.

解：符合题意的三棱锥可以有三种.

❶三棱锥S-ABC中，△SAB和△SAC是等腰直角三角形，且∠SAB=∠SAC=90°，而△ABC是边长为1的正三角形，则此三棱锥的体积是见图11-11(a).

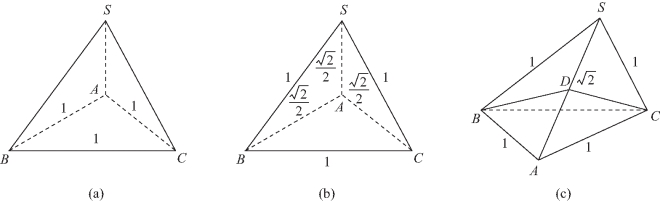
图11-11

❷三棱锥S-ABC中，△SAB和△SAC是等腰直角三角形，且∠SAB=∠SAC=90°，而△SBC是边长为1的正三角形，则此三棱锥的体积是见图11-11(b).

❸三棱锥S-ABC中，△SAB和△SAC是等腰直角三角形，且∠SBA=∠SCA=90°，而△SBC和△ABC都是边长为1的正三角形，取SA的中点D，联结BD，CD，则SA⊥BD且SA⊥CD，即SA⊥平面BCD，又则△BCD是∠BDC=90°的等腰直角三角形，此三棱锥的体积是见图11-11(c).

例3　已知斜三棱柱ABC-A1B1C1的底面是直角三角形，∠BAC=90°，且侧棱与底面成60°，求它的体积.

解题策略　在证得平面ABC⊥平面ABC1，点C1在底面上的射影H在直线AB上之后，但点H在直线AB上的位置不能确定，所以要对点H的位置分类讨论.

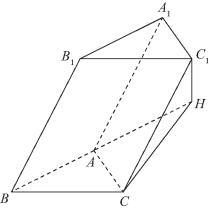
图11-12

解：∵AC⊥AB，AC⊥BC1，∴AC⊥平面ABC1.又∵AC⊂平面ABC，∴平面ABC⊥平面ABC1则点C1在平面ABC上的射影一定在直线AB上，∴过C1作C1H垂直于BA，设C1H=x.

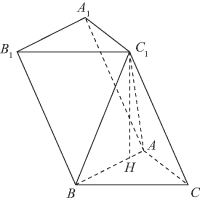
图11-13(www.xing528.com)

❶若点H在线段BA的延长线上，联结C1H，如图11-12所示，则∠C1CH是CC1与底面所成的角，即在Rt△ACH中，

在Rt△BC1H中，

解得

❷若点H在线段AB上，如图11-13所示.

在Rt△BC1H中，即解得(此时点H与点B重合).

❸若点H在线段AB的延长线上，在Rt△BC1H中，

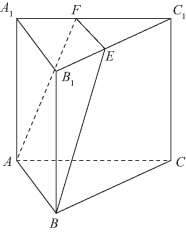
图11-14

解得不合题意.

综上所述，斜三棱柱ABC-A1B1C1的体积为或

例4　如图11-14所示，在正三棱柱ABC-A1B1C1中，过棱AB作一个与底面ABC成角的截面，求截面的面积.

解题策略　由于截面与下底面所成的二面角在内变化，以截面ABC1为界，变动中的截面可以是等腰三角形(截面ABD的顶点D在侧棱C1C上)也可以是等腰梯形(截面等腰梯形的上底EF在上底面A1B1C1内且EF∥B1A1)，故必须以此分类讨论.

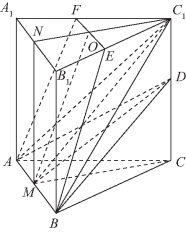
图11-15

解：如图11-15所示，在正三棱柱ABC-A1B1C1中，取AB的中点M，联结CM、C1M，CM⊥AB，C1M⊥AB，∴∠C1MC就是平面ABC1与平面ABC所成二面角的平面角，

❶当时，过AB棱的截面是等腰三角形ABD，∠DMC=θ.

截面的面积为

❷当时，过AB棱的截面是等腰梯形ABEF，其中EF∥BA.取A1B1的中点N，联结MN、C1N，C1N交EF于点O，联结OM，如图11-15所示.

∵∠OMC是截面与底面ABC所成的二面角的平面角，

∴∠OMC=θ，在正三棱柱ABC-A1B1C1中，MN=2，∠MON=θ，

∵BA∥EF，∴B1A1∥EF，在△A1B1C1中，

∴截面的面积为