解析几何问题的分类讨论法优化方法

含参数的二元二次方程表示曲线类型的判定，求轨迹方程并说明轨迹是什么曲线，从运动变化观点考察图形的变化过程，这些解析几何问题都需要对参数或选择关键节点作为分类标准，运用分类讨论法解题，解决解析几何问题的过程，是不断缩小条件与结论的差异的过程，在由条件向结论不断靠拢的实施过程中，情况的变化不是单一的，必要的分类与整合不可缺少.

例1　已知抛物线顶点在原点，焦点在坐标轴上，又知此抛物线上的一点A(m,-3)到焦点F的距离为5，则m的值为________；抛物线方程为________.

解题策略　由于抛物线的开口方向未定，根据点A(m,-3)在抛物线上这一条件，抛物线开口向下、向左、向右均有可能，以此分类讨论求解.

解： ❶若抛物线开口向下，设抛物线方程为x2=-2py(p>0)，此时准线方程为由抛物线定义知解得p=4.

∴抛物线方程为x2=-8y，这时将A(m,-3)代入方程得

❷若抛物线开口向左或向右，可设抛物线方程为y2=2ax(a≠0).

从p=|a|知准线方程为由题意知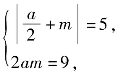解此方程组得

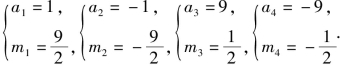
综合❶❷得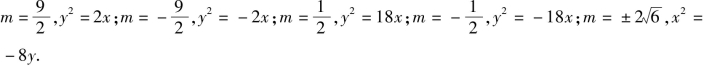

图11-9

例2　如图11-9所示，△AOB是等腰直角三角形，动直线l过点P(1,1)与△AOB的斜边、直角边分别交于不同的点M，N.

(1)设直线l的斜率为k，求k的取值范围，并用k表示点M的坐标；

(2)试写出表示△AMN的面积S的函数解析式S(k)，并求S(k)的最大值.

解题策略　由于l绕P点转动，则N点可落在OA上，也可落在OB上，S△AMN的计算不一样，所以必须对l的斜率的取值范围进行分类讨论.

解：(1)由已知条件得A(1，0)，B(0，1)，k>0，设直线l的方程为y=kx+1-k，由　得

(2)当k≥1时，点N在直角边OA上，

当0<k<1时，点N在直角边OB上，N(0，1-k).

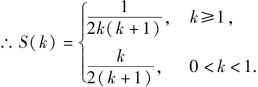
当k≥1时，S(k)递减，当0<k<1时，

综上所述，

例3　根据k的变化，讨论方程所表示的曲线的形状.

解题策略　必须将k≠4这个大区域划分成小区域或用特殊值进行分类讨论，注意不重不漏.

解：k∈R且k≠4，从k的特殊值入手讨论：

❶当k=2时，方程化为表示两条平行于y轴的直线；

❷当k=-1时，方程化为表示两条相交于原点的直线；(www.xing528.com)

❸当k≠2且k≠-1时，方程化为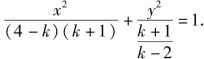

对两分母的符号再分3小类讨论：

当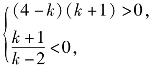即-1<k<2时，方程表示焦点在x轴上且中心在原点的双曲线；

当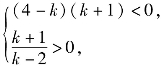即k<-1或k>4时，方程表示焦点在y轴上且中心在原点的双曲线；

当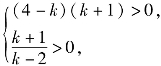即2<k<4时，

由于

∴当k=3时，方程表示圆x2+y2=4.

而当2<k<3或3<k<4时，方程表示焦点在y轴上且中心在原点的椭圆.

例4　已知椭圆的离心率为过右焦点F的直线l与C相交于A，B两点，当l的斜率为1时，坐标原点O到l的距离为

(1)求a，b的值；

(2)C上是否存在点P，使得当l绕F转到某一位置时，有成立？若存在，求出所有的点P的坐标与l的方程；若不存在，说明理由.

解题策略　第(1)问，直接运用点到直线的距离公式以及椭圆参数的有关关系式计算即得a，b的值.第(2)问，过右焦点F的直线l绕F旋转，必定会碰到斜率存在及不存在的情况，必须进行分类讨论，防止对斜率不存在这一特殊情况的疏忽，在求解过程中注意利用向量坐标关系及方程思想、韦达定理解答问题.

解：(1)设F(c，0)，当l的斜率为1时，其方程为x-y-c=0，O到l的距离为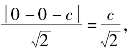故由得

(2)假设C上存在点P，使得当l绕F转到某一位置时，有成立.

由(1)知C的方程为2x2+3y2=6，设A(x1，y1)，B(x2，y2)，且F(1，0).

❶当l不垂直x轴时，设l的方程为y=k(x-1)，C上的点P使成立的充要条件是P点的坐标为(x1+x2，y1+y2)且2(x1+x2)2+3(y1+y2)2=6.

整理得

又A，B在C上，即故

2x1x2+3y1y2+3=0　　①

将y=k(x-1)代入2x2+3y2=6，并化简整理得(2+3k2)x2-6k2x+3k2-6=0.于是

代入①式解得k2=2，此时

于是即

因此，当时，的方程为

当时，的方程为

❷当l垂直于x轴时，由知，C上不存在点P使成立.

综上所述，C上存在点使成立，此时l的方程为