排列组合问题中的分类加法计数原理就是分类讨论思想的具体体现,讨论时应注意分类标准的统一,求解关于多项式与二项式的积以及两个以上二项式的和或差有关的某一项系数问题时,因不能由通项直接写出,需按条件进行分类讨论.
例1 (涂色问题)如图11-7所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,求不同的染色方法总数.
解题策略 涂色问题是计数原理应用的典型问题,是一个问题解决的策略的运用过程,正确运用计数原理是关键,分类要做到“不重不漏”,分步要正确设计分步的程序,即合理分类,正确分步.
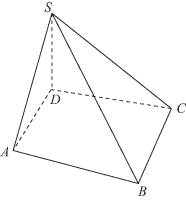
图11-7
解法一 按所有颜色种数分类.
第一类:5种颜色全用,共有![]() 种不同的方法;
种不同的方法;
第二类:只用4种颜色,则必有某两个顶点同色(A与C,或B与D),共有![]() 种不同的方法;
种不同的方法;
第三类:只用3种颜色,则A与C,B与D必定同色,共有![]() 种不同的方法,由分类计数原理,得不同的染色方法总数为
种不同的方法,由分类计数原理,得不同的染色方法总数为![]() 种.
种.
解法二 可分为两大步进行,先将四棱锥一侧面三个顶点染色,然后再分类考虑另外两个顶点的染色数,用乘法原理即可得出结论.
由题设,四棱锥S-ABCD的顶点S,A,B所染的颜色互不相同,它们共有5×4×3=60种染色方法.
当S,A,B染好后,不妨设其颜色分别为1,2,3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法.可见,当S,A,B已染好时,C,D还有7种染法,故不同的染色方法有60×7=420种.
解法三 以S,A,B,C,D顺序分步染色.
第一步:S点染色,有5种方法;
第二步:A点染色,与S在同一条棱上,有4种方法;
第三步:B点染色,与S,A分别在同一条棱上,有3种方法;
第四步:C点染色,也有3种方法,但考虑到D点与S,A,C相邻,需要针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法;当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.
由分步计数原理、分类计数原理得不同的染色方法共有:5×4×3×(1×3+2×2)=420种.
例2 (集合元素问题)(1)在1,2,3,…,30这30个数中,每次取两两不等的三个数,使它们的和是3的倍数,共有多少种不同的取法?
(2)已知集合A={1,2,3,4,5,6},B={5,6,7,8,9},从集合A中选3个元素,从集合B中选2个元素,能组成多少个含有5个元素的集合?
解题策略 本例难度较高,对于(1),首先要把30个数按被3除的状况分为三个集合,再逐一讨论元素的取法;对于(2),由于类别较多,要防止重复或遗漏.
解:(1)把这30个数分成3类,即3个集合,被3整除的数集A0={3,6,9,…,30},被3除余1的数集A1={1,4,7,…,28},被3除余2的数集A2={2,5,8,…,29}.每个集合各有10个元素,三个数的和是3的倍数的取法有两类:
第一类:在同一集合内取三个数,取法为![]()
第二类:每个集合内各取一个数,取法为![]()
根据加法原理,所求取法种数为![]() 种.
种.
(2)由于A∩B={5,6},而由集合元素的无序性及互异性,可判断这是组合问题,因元素不能重复,故应对5和6这两个元素分别进行讨论.
❶不选5和6,则有![]() 种.
种.
❷在{5,6}中选1个,则
在{1,2,3,4}中选2个,在{7,8,9}中选2个,共有![]() 种;
种;
在{1,2,3,4}中选3个,在{7,8,9}中选1个,共有![]() 种.
种.
❸在{5,6}中选2个,则
在{1,2,3,4}中选1个,而在{7,8,9}中选2个,共有![]() 种;
种;
在{1,2,3,4}中选2个,而在{7,8,9}中选1个,共有![]() 种;
种;
在{1,2,3,4}中选3个,而在{7,8,9}中不选,共有![]() 种.
种.
综上所述,根据加法原理,共有
![]() 种.(https://www.xing528.com)
种.(https://www.xing528.com)
即共有106个含有5个元素的集合.
例3 已知![]() 的展开式中,第k,k+3两项的二项式系数相等,其中2<k<5(k,n∈N*),求展开式的前三项的系数之和及中间项的系数.
的展开式中,第k,k+3两项的二项式系数相等,其中2<k<5(k,n∈N*),求展开式的前三项的系数之和及中间项的系数.
解题策略 在本例的解题过程中必须对k和相应n的取值分类讨论.
解:由题意![]() 或k=4.
或k=4.
(1)当k=3时,n=7,原二项式为![]()
![]() 的展开式中的前三项的系数之和为
的展开式中的前三项的系数之和为![]()
∵n=7,∴展开式中共有8项,中间两项分别是第4项、第5项.
∴中间项的系数分别为![]()
(2)当k=4时,n=9,原二项式为![]()
![]() 的展开式中的前三项的系数之和为
的展开式中的前三项的系数之和为![]()
∵n=9,∴展开式中的中间两项是第5项、第6项,系数分别为![]()
例4 设An={x|2n<x<2n+1,且x=3m,其中m,n∈N*}.
(1)求An中的最大数和最小数;
(2)求An中所有元素之和Sn;
(3)求![]()
解题策略 这是一道综合题,是集合、数列与二项式定理等知识的交汇,要搞清An中元素的特征,须从研究2n,2n+1与3的关系着手,而2n=(3-1)n,此时二项式定理这一解题工具就找到用武之地了,由于展开之后必出现(-1)n,故对n是奇数还是偶数进行分类讨论,从而化整为零,各个击破的策略也已成定局.
解:(1)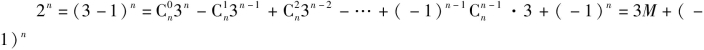 (M为整数).
(M为整数).
❶当n=2k-1时,2n=3M1-1,故2n+1是3的倍数.
即2n+1是An中的最小数,此时,n+1=2k.
故2n+1=3M2+1,即2n+1-1=3M2.
∴2n+1-1也是An中的元素,且是An中的最大数.
❷当n=2k时,2n=3M3+1,故2n-1是3的倍数.
∴2n-1+3=2n+2是3的倍数,即2n+2是An中的最小数.
此时n+1=2k+1,故2n+1=3M4-1,即2n+1+1是3的倍数.
2n+1+1-3=2n+1-2是3的倍数,即2n+1-2是An中的最大数.
综上所述,n为奇数时,An中的最小数为2n+1,最大数为2n+1-1;n为偶数时,An中的最小数为2n+2,最大数为2n+1-2.
(2)由于An中各数是以3为公差的等差数列,因此可用等差数列求和公式求解.
当n为奇数时,An中各数是以2n+1为首项、3为公差、2n+1-1为末项的等差数列,设项数为k1,则有
2n+1-1=2n+1+3(k1-1),解得![]()
![]()
当n为偶数时,An中元素是以2n+2为首项、3为公差、2n+1-2为末项的等差数列,设项数为k2,则有
2n+1-2=2n+2+3(k2-1),解得![]()
![]()
综上所述,Sn=22n-1+(-1)n-1·2n-1,n∈N*.
(3)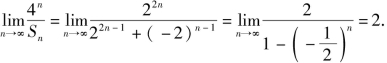
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




