利用分类讨论法优化数列问题解答

运用分类与整合的思想方法解数列问题的类型主要如下.

(1)在数列中已知Sn，求数列的通项公式an时，要注意对n=1的验证.因为在an与Sn的关系中，an=Sn-Sn-1成立的条件是n≥2,求an时切勿漏掉n=1，即a1=S1的情况.

(2)等比数列求和时，若公比q为参数，则需分q=1和q≠1两类进行求和.

(3)求数列{|an|}的前n项和时，为脱去绝对值号，需确定an≥0(或an≤0)而进行分类讨论.

(4)对于通项公式为分段形式给出或前n项和因奇偶性不同而不同的数列，应分类讨论.

例1　(1)已知数列{an}的通项公式为设Sn是数列{an}的前n项和，若bn-λSn>0对任意n∈N*都成立，则实数λ的取值范围是________；

(2)数列{an}中，a1=1,a2=2,数列{an·an+1}是公比为q(q>0)的等比数列，求数列{an}的前2n项的和S2n.

解题策略　第(1)问，由于数列{an}的通项公式中含有(-1)n，且bn=anan+1，则在求bn-λSn的表达式时必定要对n是正奇数或正偶数分两类求解；第(2)问，由{an,an+1}是等比数列，可得{an}的奇数项、偶数项分别成等比数列，求和时还要对q≠1,q=1进行分类讨论.

解：(1)

❶当n是正奇数时，

即λ<(2n+1)对任意正奇数n恒成立，又单调递增，

故当n=1时，(2n+1)有最小值1，即λ<1.

❷当n是正偶数时，

即又2n-1>0，故对任意正偶数n都成立，又随n增大而增大，故当n=2时，有最小值即综合❶ ❷可知λ<1.

(2)由数列{anan+1}是公比为q的等比数列，得这表明数列{an}的所有奇数项成等比数列，所有偶数项成等比数列，且公比都是q，

又∵a1=1,a2=2.

则当q≠1时，S2n=a1+a2+a3+a4+…+a2n-1+a2n

=(a1+a3+a5+…+a2n-1)+(a2+a4+a6+…+a2n)

当q=1时，S2n=a1+a2+a3+a4+…+a2n-1+a2n

=(a1+a3+a5+…+a2n-1)+(a2+a4+a6+…+a2n)

=(1+1+1+…+1)+(2+2+2+…+2)=3n.

例2　已知数列{an}的通项公式且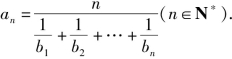

(1)求数列{bn}的通项公式；

(2)求数列中最大值的项和最小值的项.

解题策略　已知数列前n项和的形式，求通项公式时必须对n≥2或n=1分类讨论，若数列的通项为分段形式，则必须分类求最值再整合.

解：(1)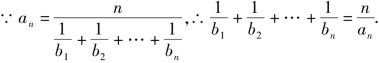

当n=1时，

当n≥2时，

∴bn=n(n+1).

综上，

(2)当n=1时，

当n≥2时，

∵f(n)=4n2+4n+1在n≥2时为增函数，∴必有4n2+4n+1≥25.

由可知

数列的最大值项为最小值项为

例3　已知等差数列{an}的公差为2，前n项和为Sn，且S1,S2,S4成等比数列.

(1)求数列{an}的通项公式；

(2)令求数列{bn}的前n项和Tn.

解题策略　本例的难点在第(2)问，数列{bn}的通项中含有(-1)n-1，则势必要在求{bn}的前n项和Tn时对n分偶数、奇数讨论，由于已知{an}为等差数列，则anan+1为等差数列连续两项之积且在分母上，能否裂项求和出现邻项相消的情况，(-1)n-1对此有何影响，是否需要根据n的奇偶性进行分类？裂项求和是数列求和的重要方法之一，裂项求和的数列是否一定与等差数列相关？比如裂项成功，但在数列通项中完全找不到等差数列的“身影”.又比如同样裂项成功，可见裂项求和并不局限于与等差数列相关的题型，只要数列的通项能转化成的结构模式都是可以的，仿佛这是题外话，与本题的解答并无直接关系，但数学核心素养就是在对问题的不断发散思维中提高的.本例中由于出现了(-1)n-1,似乎必须对n分奇、偶数讨论，但并不仅限于此，也可以利用数学归纳法求解，以避开分类讨论.(www.xing528.com)

解：(1)由题意得(2a1+2)2=a1(4a1+12),解得a1=1,∴an=2n-1.

(2)解法一

观察分子和分母的特点会发现(2n-1)+(2n+1)=4n.

于是

此时，数列{bn}的前n项和

看来能出现邻项相消了，但是式子末端的剩余项却不能确定，原因在于还存在(-1)n-1正负取值不确定，这自然就会想到要进行分类讨论，根据n的奇偶性进行分类，则有：

当n为偶数时，有

当n为奇数时，有

故

实际上，在上述通项变换中出现的并不是常规的邻项相消，但借助(-1)n-1同样产生了“正负相间”的效果，达到消项求和的目的.

解法二

T2

…

于是猜想得出

下面用数学归纳法证明：

❶当n=1时，由上述推理可知猜想成立；

❷假设当n=k(k∈N*)时猜想成立，即成立.

而

于是，当n=k+1时，Tk+1

也就是说当n=k+1时猜想也成立.

综合❶❷可知对任意的n∈N*，猜想都成立，

即

例4　已知数列{an}和{bn}满足：其中λ为实数，n为正整数.

(1)试判断数列{bn}是否为等比数列，并证明该结论；

(2)设0<a<b，Sn为数列{bn}的前n项和，是否存在实数λ,使得对任意正整数n，都有a<Sn<b？若存在，求λ的取值范围；若不存在，说明理由.

解题策略　分类讨论是解决问题的一种逻辑方法，在简化研究对象、发展思维方面起着重要作用，在本例的解答中有两处是一定要讨论的，一是对等比数列的证明一定要关注首项不可为0，二是对n分正奇数、正偶数的讨论.

解：(1)∵bn+1

且b1=-(λ+18).

∴当λ=-18时，b1=0(n∈N*)，此时{bn}不是等比数列；

当λ≠-18时，数列{bn}是以-(λ+18)为首项，为公比的等比数列.

(2)由(1)知，当λ=-18时，b1=0,Sn=0.不满足题目要求.

∴λ≠-18,故可得要使a<Sn<b对任意正整数n成立,

即得

　　①

令则当n为正奇数时，当n为正偶数时，的最大值为的最小值为于是，由①式得

当a<b≤3a时，由-b-18≥-3a-18知不存在实数λ满足题目要求；

当b>3a时，存在实数λ,使得对任意正整数n，都有a<Sn<b，且λ的取值范围是(-b-18,-3a-18).