在讨论两个复数集关系时,涉及参数,就需要分类讨论,复数集内解一元二次方程,必须按判别式分类求解,运用平面向量研究几何图形的性质也常常需要对图形的某一元素的变化分类与整合.
例1 设x1,x2是方程2x2+3ax+a2-a=0(a∈R)在复数范围内的两根,求|x1|+|x2|(用含a的解析式表示).
解题策略 在复数集内解一元二次方程,必须对Δ>0,Δ<0分类求解,在去掉绝对值号时又需进一步对a的取值进行分类讨论.
解:若Δ=9a2-8a2+8a≥0,即a≥0或a≤-8.此时x1,x2∈R.
|x1|+|x2|![]()
由a2-a≥0得a≥1或a≤0,
∴当a≥1或a≤-8时,![]()
当0≤a<1时,![]()
若Δ=9a2-8a2+8a<0,即-8<a<0,此时,x1,x2为一对共轭虚根.
综上所述,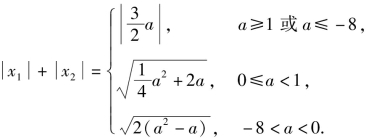
例2 设两复数集M={z|z=m+i(4-m2),m∈R},N={z|z=2cosθ+i(λ+3sinθ),θ∈R}.
(1)若M∩N≠∅,求实数λ的取值范围;
(2)当实数λ在(1)中变化时,进一步讨论集合M∩N的元素个数,并当λ取定值时,求M∩N;
(3)本题的几何意义是什么?
解题策略 第(1)问,M∩N≠∅,即两集合有公共元素,利用两复数相等的充要条件,消去m,即可得λ关于sinθ的三角函数,进而求值域.第(2)问,可通过函数与方程的思想方法结合方程根的情况进行分类讨论,分类要全面,防止遗漏.第(3)问,求出集合M,集合N在复平面上的点的轨迹,把数的问题转化为形的问题,其中集合N对应的轨迹含参数λ,当λ变化时,该曲线在运动,从而本题探求的是两曲线相交的不同情况.本例涉及函数与方程、分类与整合、数形结合等多种数学思想,是一道既具新颖性又具典型性的好题.
解:(1)由M∩N≠∅,得z=m+i(4-m2)=2cosθ+i(λ+3sinθ).
![]() 消去m,得
消去m,得![]()
由-1≤sinθ≤1,得![]()
(2)由4sin2θ-3sinθ-λ=0,令sinθ=t,考虑f(t)=4t2-3t-λ,t∈[-1,1].
❶当![]() 此时,
此时,![]() 而
而![]()
此时集合M∩N有2个元素![]()
❷当f(-1)·f(1)<0![]() 1<λ<7.
1<λ<7.
此时,sinθ在(-1,1)内有一解,而![]() 有两解.
有两解.
此时集合M∩N有两个元素.
❸当f(-1)=0![]() λ=7,此时有4t2-3t-7=0,即(4t-7)(t+1)=0,
λ=7,此时有4t2-3t-7=0,即(4t-7)(t+1)=0,
![]() (舍),sinθ=t2=-1.
(舍),sinθ=t2=-1.
∴cosθ=0,此时M∩N有1个元素M∩N={4i}.
❹当f(1)=0![]() λ=1.此时有4t2-3t-1=0,即(4t+1)(t-1)=0,
λ=1.此时有4t2-3t-1=0,即(4t+1)(t-1)=0,
![]() 当
当![]() 时,
时,![]() 当sinθ=1时,cosθ=0.
当sinθ=1时,cosθ=0.
❺当 此时M∩N有4个元素.(https://www.xing528.com)
此时M∩N有4个元素.(https://www.xing528.com)
(3)令z=x+yi知,集合M在复平面上的点的轨迹为抛物线x2=-(y-4),集合N在复平面上的点的轨迹为椭圆![]()
故本题讨论的是,当λ变化时,椭圆上下移动与抛物线相交的不同情况.
例3 已知![]() 求△ABC为等腰直角三角形的充要条件.
求△ABC为等腰直角三角形的充要条件.
解题策略 直角顶点未明确,必须对哪一角为直角进行分类讨论.
解:❶当∠CAB=90°,AB=AC时,△ABC为等腰直角三角形.
此时![]() 且
且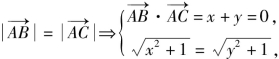 解得x+y=0.
解得x+y=0.
❷当∠CBA=90°,BA=BC时,△ABC为等腰直角三角形.
此时,![]() 且
且![]()
![]() 由
由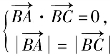
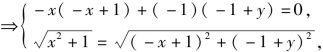 解得
解得![]() 或
或![]()
❸当∠BCA=90°,CA=CB时,△ABC为等腰直角三角形.
此时![]() 且
且![]() 由
由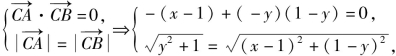 解得
解得![]() 或
或![]()
综上所述,△ABC为等腰直角三角形的充要条件是x+y=0或![]() 或
或![]() 或
或![]() 或
或![]()
例4 在△ABC中,![]() 点A(1,1).
点A(1,1).
(1)若C(2,0),且A,B,C能构成直角三角形,求点B的坐标;
(2)x轴上是否存在点B,C满足![]() 若存在,求出点B,C的坐标;若不存在,请说明理由.
若存在,求出点B,C的坐标;若不存在,请说明理由.
解题策略 第(1)问,必须对△ABC中哪一个角是直角进行分类讨论,即使某角不可能是直角,也应当说明理由;第(2)问,点B,C在x轴上的位置关系未定,也会有两种不同的情况.
解:(1)设点B(x,y),则![]()
当∠A=90°时,![]() 得x-y=0,
得x-y=0,
又∵(x-2)2+y2=4,∴x=0或2.
∴点B的坐标为(0,0)或(2,2).
当∠C=90°时,![]() 得x-2-y=0.
得x-2-y=0.
又![]()
∴点B的坐标为![]() 或
或![]()
综上所述,点B的坐标为(0,0)或(2,2)或![]() 或
或![]()
(2)依题意可设点B(b,0),C(c,0),则![]()
∵![]()
∴b=0或b=2.∴点B,C的坐标分别为(0,0),(2,0)或(2,0),(0,0).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




