运用分类讨论法解决三角函数问题

在研究三角函数的图像及其性质过程中，在处理解三角形题型时，都需要运用分类与整合的思想方法.

例1　若函数f(x)=a+bcosx+csinx的图像经过点(0,1)和且当时，|f(x)|≤2恒成立，则实数a的取值范围是________.

解题策略　由f(x)的图像经过(0,1)和两点的条件消去b和c，使原函数含有单参数a，在后续的解题过程中必须对a的取值分类讨论.

解：∵f(x)经过点(0,1)和故

f(x)=a+(1-a)cosx+(1-a)sinx=a+(1-a)(sinx+cosx)

❶当a<1时，1-a>

要使-2≤f(x)≤2恒成立，只要

即又a<1,从而

❷当a=1时，f(x)=1∈[-2,2];

❸当a>1时，

要使-2≤f(x)≤2恒成立，只要

解得又a>1,从而

综上所述，a的取值范围为

例2　已知f(x)=2acosxsin(x+θ)+2asinx(cosxcosθ-sinxsinθ),θ∈(0,2π).若且f(x)在上为减函数.

(1)求函数f(x)的最小正周期；

(2)求实数a和角θ的值.

解题策略　在研究三角函数y=Asin(ωx+φ)的性质时，当A的正负未定时，则必须对A的正、负进行分类讨论.

解：(1)f(x)=2acosxsin(x+θ)+2asinx(cosxcosθ-sinxsinθ)

=2acosxsin(x+θ)+2asinxcos(x+θ)f(x)=2asin(2x+θ).

显然a≠0，∴f(x)的最小正周期为

(2)若a>0，f(x)在上为减函数，且的最大值为2，即a=1，此时f(x)=2sin(2x+θ).

若a<0，同理a=-1，此时f(x)=-2sin(2x+θ).

综上所述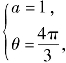或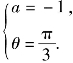

图11-1

例3　如图11-1所示，有一块等腰三角形形状的空地ABC,腰CA的长为3，底AB的长为4，现决定在该空地内筑一条笔直的小路EF(宽度不计)，将该空地分成一个四边形和一个三角形，设分成的四边形和三角形的周长相等，面积分别为S1和S2.

(1)若小路一端E为AC的中点，求此时小路的长度；

(2)求的最小值.

解题策略　本例引起分类讨论的是小路端点E，F的位置，位置的可能性以及位置不同导致结论的变化.

解：(1)先确定点F的位置.

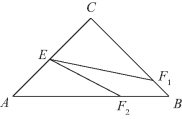
图11-2

❶若点F在BC上(如图11-2中F1位置).(www.xing528.com)

设CF1=t,则EC+CF1=AE+AB+BF1,即得(舍去)，故点F不在BC上.

❷若点F在AB上(如图11-2中F2位置)，设BF2=t,则EC+BC+BF2=AE+AF2,即得此时于是在△AEF2中，得故若小路一端E为AC的中点，此时小路的长度为

图11-3

(2)分情况讨论点E，F的位置.

❶若小路的端点E，F都在两腰上(如图11-3所示)，

设CE=x,CF=y,则EC+CF=AE+AB+BF,即x+y=(3-x)+4+(3-y),得x+y=5(0<x<3,0<y<3).

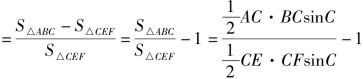
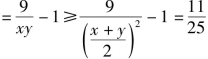
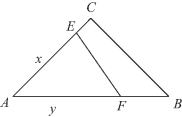
图11-4

❷若小路的端点E,F分别在一腰(不妨设在腰AC上)和底边上(如图11-4所示)，设AE=x,AF=y,由AE+AF=BC+CE+BF,即x+y=(3-x)+3+(4-y),得x+y=5(0<x<3,0<y<4).

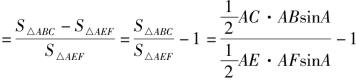
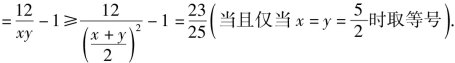
综上所述，的最小值为

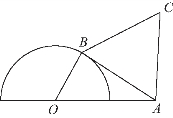
图11-5

例4　如图11-5所示，半圆O的直径为2，点A为直径延长线上的一点，OA=2,点B为半圆上任意一点，以AB为边向半圆外作等边三角形ABC.

(1)求四边形OACB的面积的最大值；

(2)求线段OC长的最大值.

解题策略　求解时，若设∠AOB=α,则必须对α为锐角、钝角、直角的情况分类讨论，如图11-6所示.

解：(1)设∠AOB=α,则α∈(0,π),在△AOB中，AB2=OB2+OA2-2OB·OAcosα=1+4-2×1×2cosα=5-4cosα.

于是S四边形OACB

=

又∵0<α<π，∴当即时，S四边形OACB取到最大值，

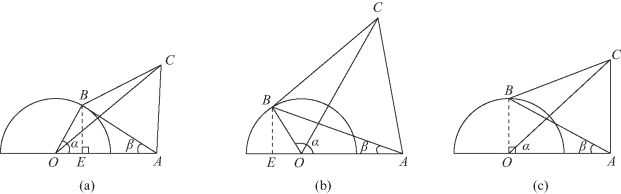
图11-6

(2)设∠AOB=α,∠OAB=β.

❶若α为锐角，见图11-6(a)，则OBsinα=ABsinβ且

OBcosα+ABcosβ=2,∴ABsinβ=sinα,ABcosβ=2-cosα.

❷若α为钝角，见图11-6(b)，则OBsin(π-α)=ABsinβ,且ABcosβ-OBcos(π-α)=2,∴ABsinβ=sinα,ABcosβ=2-cosα.

❸若α为直角，见图11-6(c),则仍有ABsinβ=sinα,ABcosβ=2-cosα.

于是在△AOC中，OC2

=

∵0<α<π,∴当即时，OC取得最大值3.