运用分类讨论法解含参数的函数、方程、不等式问题

在求解函数、方程、不等式问题中，由于含有参数，而参数取不同值时会导致不同的结果，因而需要对参数进行分类讨论，即选择一个标准，依次分成几个能用不同形式去解决的小问题，从而使问题获得解决，体现了化整为零、各个击破、积零为整——即分类与整合的思想.

例1　设a为实数，函数f(x)=x2+|x-a|+1,x∈R.

(1)讨论f(x)的奇偶性；

(2)求f(x)的最小值.

解题策略　讨论函数的奇偶性必须对a=0和a≠0进行分类讨论，去掉绝对值符号必须对x≤a和x≥a进行分类讨论，求函数的最值又必须进一步对a的取值与二次函数对称轴的关系进行分类讨论，三次讨论层层深入.

解：(1)当a=0时，f(-x)=(-x)2+|-x|+1=f(x),此时f(x)为偶函数，

当a≠0时，f(a)=a2+1,而f(-a)=a2+2|a|+1,

∴f(-a)≠f(a),f(-a)≠-f(a).

∴此时函数f(x)既不是奇函数，也不是偶函数.

(2)对|x-a|去掉绝对值号进行讨论：

① 当x≤a时，

若则f(x)在(-∞,a]上单调递减，

∴f(x)在(-∞,a]上最小值为f(a)=a2+1.

若则f(x)在(-∞,a]上的最小值为且

② 当x≥a时，

若则f(x)在[a,+∞)上的最小值为且

若则f(x)在[a,+∞)上单调递增，

∴f(x)在[a,+∞)上的最小值为f(a)=a2+1.

综上所述，当时，f(x)的最小值为当时，f(x)的最小值为a2+1;当时，f(x)的最小值为

例2　(1)若lg(kx)=2lg(x+1)仅有一个实数根，那么k的取值范围是________;

(2)函数求使y为负值的x的取值范围.

解题策略　第(1)问是含参数的对数方程仅有一个实根，求参数的取值范围，首先转化为方程与不等式的混合组，而所得的是含参数的一元二次方程.由判别式结合混合组中两个不等式进行分类讨论，从而获解.第(2)问，当原问题转化为指数不等式时，必须对底数的取值在(0,1)还是(1,+∞)进行分类讨论，别忘了特殊情况a=b>0的讨论.

解：(1)由题意知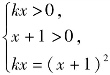即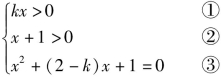

对③式由求根公式得　　④

Δ=k2-4k≥0k≤0或k≥4(k=0不合题意，应舍去).

❶当k<0时，由③式得同为负根.又由④式知方程有一个解x1.

❷当k=4时，原方程有一个解

❸当k>4时，由③式得同为正根且x1≠x2,不合题意，舍去.

综上可得，k<0或k=4为所求.

(2)即a2x+2axbx-b2x>0.

两边同除以b2x，得或

若a>b>0,则

若a=b>0,则而

若0<a<b,则

综上所述，当a>b时，时，x∈R；a<b时，

例3　(1)已知函数y=f(x)的图像与函数y=ax(a>0且a≠1)的图像关于直线y=x对称，记g(x)=f(x)[f(x)+f(2)-1],若y=g(x)在区间上是增函数，则实数a的取值范围是(　　).

(2)关于x的方程(x2-1)2-|x2-1|+k=0,给出下列4个命题：

① 存在实数k，使得方程恰有2个不同的实根；

② 存在实数k，使得方程恰有4个不同的实根；

③ 存在实数k，使得方程恰有5个不同的实根；

④ 存在实数k，使得方程恰有8个不同的实根.

其中假命题的个数是(　　).

A.0　　　B.1　　　C.2　　　D.3(www.xing528.com)

解题策略　第(1)问，由于底数a未确定，必须对a的值在(0,1)还是(1,+∞)进行分类讨论，若采用换元法，则必须在a的不同范围内结合对数函数单调性确定新元的范围；第(2)问，若考虑去掉绝对值符号，则必须对x的取值范围分类讨论，在进一步解答过程中又必须对参数k的取值分类讨论.

解：(1)已知函数y=f(x)的图像与函数y=ax(a>0且a≠1)的图像关于直线y=x对称，则f(x)=logax.

记g(x)=f(x)[f(x)+f(2)-1]=(logax)2+(loga2-1)logax.

❶当a>1时,y=g(x)在区间上是增函数,y=logax为增函数，令要求对称轴矛盾；

❷当0<a<1时，y=g(x)在区间上是增函数,y=logax为减函数,令要求对称轴解得数a的取值范围是故选D.

(2)解法一　关于x的方程(x2-1)2-|x2-1|+k=0可化为

(x2-1)2-(x2-1)+k=0(x≥1或x≤-1)　　①

或(x2-1)2+(x2-1)+k=0(-1<x<1)　　　②

❶当k=-2时，方程①的解为方程②无解，原方程恰有2个不同的实根；

❷当时,方程①有两个不同的实根方程②有两个不同的实根即原方程恰有4个不同的实根；

❸当k=0时，方程①的解为方程②的解为x=0,原方程恰有5个不同的实根；

❹当时,方程①的解为方程②的解为即原方程恰有8个不同的实根，故选A.

解法二　根据题意，可令|x2-1|=t(t≥0),则原方程化为t2-t+k=0　　①

作出函数t=|x2-1|的图像，结合函数的图像可知，当t=0或t>1时原方程有两个不同的根；当0<t<1时，原方程有4个根；当t=1时，原方程有3个根，于是：

❶当k=-2时，方程①有一个正根t=2,相应的原方程的解有2个;

❷当时，方程①有两个相等的正根相应的原方程的解有4个；

❸当k=0时，方程①有两个不等根t=0或t=1，故此时原方程有5个根；

❹当时，方程①有两个不等正根，且此时方程①有两个正根且均小于1，故相应满足原方程的解有8个，故选A.

例4　已知函数f(x)=xe-x+(x-2)ex-a(e≈2.72).

(1)当a=2时，证明：函数f(x)在R上是增函数；

(2)若a>2时，当x≥1时，恒成立，求实数a的取值范围.

解题策略　本例是含参数的函数的单调性问题与含参数不等式恒成立问题.第(1)问，在证明单调性过程中对x的取值分类讨论；第(2)问，为了解决含参数不等式恒成立问题，必须研究新构造的函数的单调性和极值，必须对参数a的取值范围分类讨论，分类要合理，不重不漏，符合最简原则.总之，分类讨论思想的本质是“化整为零，积零为整”，思维策略与操作过程是：明确讨论的对象和动机→确定分类的标准→逐类进行讨论→归纳结论→检验分类是否完备(即分类对象彼此交集为空集，并集为全集).

解：(1)证明　当a=2时，f(x)=xe-x+(x-2)ex-2，f(x)的定义域为R.

f′(x)=e-x-xe-x+ex-2+(x-2)ex-2=(x-1)(ex-2-e-x)

=e-x(x-1)(ex-1-1)(ex-1+1).

当x≥1时，x-1≥0,ex-1-1≥0,∴f′(x)≥0;

当x<1时，x-1<0,ex-1-1<0,∴f′(x)≥0.

∴对任意实数x,f′(x)≥0，∴f(x)在R上是增函数.

(2)当x≥1时，恒成立，即(x-2)e2x-a-x2+3x-1≥0恒成立.

设h(x)=(x-2)e2x-a-x2+3x-1(x≥1),则h′(x)=(2x-3)(e2x-a-1).

令(2x-3)(e2x-a-1)=0,解得

❶当即2<a<3时，有

∴要使结论成立，则

即

解得

❷当即a=3时，h′(x)≥0恒成立，∴h(x)是增函数，又h(1)=-e-1+1>0,故结论成立；

❸当即a>3时，有

∴要使结论成立，则

即e2-a≤1，a2-8a+12≤0.

解得a≥2,2≤a≤6,∴3<a≤6.

综上所述，若a>2时，当x≥1时，恒成立，实数a的取值范围是