分类讨论：重要解题策略

分类讨论是数学中一种重要的思想方法，也是一种重要的解题策略，特别是对于含参数字母的问题，由于这类问题的结论大多数是随参数的变化而变化的，故问题的解答不唯一，因此，当解题进行到某一步后不能再以同一方式处理或统一的形式叙述，这时就必须根据参数字母不同的取值范围区别对待，即必须在参数字母总的取值范围(全集)内正确划分成若干个分区域(子集)，在各个分区域内方能继续进行解题，有些含参数讨论题，由于所含的参数不止一个，故这类问题要通过多级分类逐级讨论，即在每一个类中还可以继续划分更小的类，直到每一类中能使问题得到解决为止.当然，分类讨论不局限于字母参数，也有对具体问题可能出现的不同情况进行分类.

数学之美在于简捷，分类要力求简捷.

分类讨论的解题步骤如下：

(1)确定讨论的对象；

(2)确定讨论对象的取值范围(全集)；

(3)划分子区域(子集)；

(4)对于参数字母多于一个的问题则要进行逐级分类，解题时要特别注意讨论的层次，避免重复讨论或讨论不全等现象；

(5)对每个子区域讨论的结果整合起来作出结论.

其中第(5)步非常重要，分类是把整体化为部分，整合是把各部分加以归纳总结，有“分”必有“合”，因为我们研究的是问题的全体，所以必须做到有“分”有“合”，先“分”后“合”，这不仅是分类与整合的思想解决数学问题的主要过程，也是分类与整合思想的本质属性，数学思维应当注重过程的严谨性与周密性.

使用分类讨论思想解题时应当注意以下几点：

(1)要有明确的分类标准，所选择的分类标准不同就会有不同的分类方向，尽量合理分类，并选择简捷明快的方法.

(2)一旦选定一种分类标准，就必须从同一标准出发，对讨论对象分类层次分明，不重不漏.

(3)当讨论的对象不止一种时，应分层次进行，分大类时有一个统一的标准，每一大类中再分几小类另有统一的标准.

(4)注意把握问题发展的本质趋向，根据解题形势发展的需要，选择分类讨论的时机.

(5)在重视分类讨论思想应用的基础上，应防止“逢参就论”的倾向，能整体处理，可避免讨论的则尽量避开，才是解题的上策.

本讲就从近年来的高考真题来看分类讨论思想方法在解题中的重要作用.

例1　(2018年高考数学全国卷Ⅲ第21题)

已知函数f(x)=(2+x+ax2)ln(1+x)-2x.

(1)若a=0,证明：当-1<x<0时，f(x)<0;当x>0时，f(x)>0;

(2)若x=0是f(x)的极大值点，求a.

解题策略　第(1)问通过求导研究函数的单调性即可证明；第(2)问，根据函数取得极值的条件，建立关于a的式子求解.在求解过程中，两问都需要实施分类讨论，第(1)问需要对自变量的取值范围进行分类讨论，第(2)问必须对参数a的取值范围进行分类讨论.

解：(1)证明　当a=0时，

设函数则

当-1<x<0时，g′(x)<0;当x>0时g′(x)>0.

故当x>-1时，g(x)≥g(0)=0,

且仅当x=0时，g(x)=0,从而f′(x)≥0,且仅当x=0时，f′(x)=0，

∴f(x)在(-1,+∞)单调递增.

又∵f(0)=0,故当-1<x<0时，f(x)<0;当x>0时，f(x)>0.

(2)❶若a≥0,由(1)知，当x>0时，f(x)≥(2+x)ln(1+x)-2x>0=f(0),

这与x=0是f(x)的极大值点矛盾.

❷若a<0,设函数

由于当时，2+x+ax2>0,故h(x)与f(x)符号相同.

又h(0)=f(0)=0,故x=0是f(x)的极大值点.

当且仅当x=0是h(x)的极大值点，

如果6a+1>0,则当且时，h′(x)>0,故x=0不是h(x)的极大值点.

如果6a+1<0,则a2x2+4ax+6a+1=0存在根x1<0,故当x∈(x1,0),且|x|<时，h′(x)<0,故x=0不是h(x)的极大值点.

如果6a+1=0，则则当x∈(-1,0)时,h′(x)>0;当x∈(0,1)时，h′(x)<0,∴x=0是h(x)的极大值点，从而x=0是f(x)的极大值点.

综上，

例2　已知{an}是首项为2,公比为的等比数列，Sn为它的前n项和.

(1)用Sn表示Sn+1;

(2)是否存在正整数c和k，使得成立.

解题策略　本例第(2)问属于探索性问题，解题时需要灵活运用分类讨论的思想，由于题中含有双参数k，c,必须轮流分类讨论，应注意思路清晰、讨论到位.

解：(1)由得

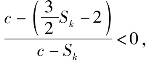(2)要使>2,只要(www.xing528.com)

故只要　　①

又Sk<4,故要使①式成立，c只能取2或3.

当c=2时，∵S1=2,∴当k=1时，c<Sk不成立.从而①式不成立.

当k≥2时，由Sk<Sk+1(k∈N*)得

故当k≥2时，从而①式不成立.

当c=3时，∵S1=2，S2=3.∴当k=1，k=2时，c<Sk不成立，从而①式不成立.

又当k≥3时，从而①式不成立.

综上所述，不存在正整数c和k，使成立.

例3　设m∈R,在平面直角坐标系中，已知向量向量动点M(x,y)的轨迹为E.

(1)求轨迹E的方程，并说明该方程所表示曲线的形状；

(2)已知证明：存在圆心在原点的圆，使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点)，并求出该圆的方程；

(3)已知设直线l与圆C：x2+y2=R2(1<R<2)相切于A1，且l与轨迹E只有一个公共点B1，当R为何值时，|A1B1|取得最大值？并求出最大值.

解题策略　第(1)问，在求得的轨迹方程中显然含有参数m，必须对m的取值分类讨论确定其轨迹；第(2)问，由于是任意一条切线，必定要对其斜率存在与否进行分类讨论；第(3)问，引入直线必然含有双参数，且圆C中尚有参数R，由于解题得法，反而避免了分类讨论.

解：(1)

即mx2+y2=1.

当m=0时，方程表示两直线，方程为y=±1;

当m=1时，方程表示的是圆；

当m>0且m≠1时，方程表示的是椭圆；

当m<0时，方程表示的是双曲线.

(2)当时，轨迹E的方程为设圆心在原点的圆的一条切线为y=kx+t,解方程组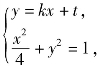得x2+4(kx+t)2=4.

即(1+4k2)x2+8ktx+4t2-4=0.

要使切线与轨迹E恒有两个交点A，B，则

Δ=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)>0，即4k2-t2+1>0,亦即t2<4k2+1,且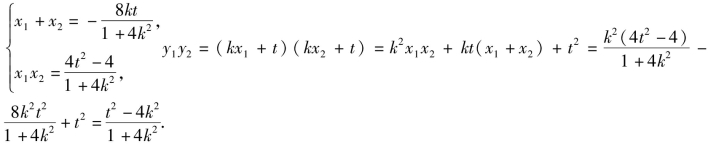

要使需使x1x2+y1y2=0.即

∴5t2-4k2-4=0,即5t2=4k2+4且t2<4k2+1,亦即4k2+4<20k2+5恒成立.

又∵直线y=kx+t为圆心在原点的圆的一条切线，∴圆的半径为

所求的圆为

当切线的斜率不存在时，切线为与交于点或也满足OA⊥OB.

综上所述，存在圆心在原点的圆使得该圆的任意一条切线与轨迹E恒有两个交点A，B，且

(3)当时，轨迹E的方程为设直线l的方程为y=kx+t.

∵直线l与圆C:x2+y2=R2(1<R<2)相切于A1,

由(2)知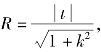即

t2=R2(1+k2)　　①

∵l与轨迹E只有一个公共点B1,由(2)知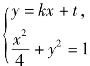得x2+4(kx+t)2=4,

即(1+4k2)x2+8ktx+4t2-4=0有唯一解，则

Δ=64k2t2-16(1+4k2)(t2-1)=16(4k2-t2+1)=0,即4k2-t2+1=0　　②

由①②得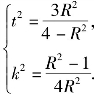此时，A，B重合为点B1(x1,y1).

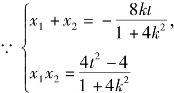中

∵点B1(x1,y1)在椭圆上，故

在直角三角形OA1B1中，

当且仅当时取等号，∴≤5-4=1.

即当时，|A1B1|取得最大值，最大值为1.