构造整体法：从细节到整体的优化方法

在解题过程中，有时可将局部的问题通过适当的增添补形得出某一整体或通过构造出若干整体表示，使问题容易解决，这种方法称为构造整体的思想方法.

例1　不查表，求A=sin1°sin3°sin5°…sin89°的值.

解题策略　本题要直接求A的值是困难的，可以将A看作局部，构造整体B=sin1°sin2°sin3°…sin89°,把原问题转化为求整体B，可巧妙地得到A的值.

解：设B=sin1°sin2°sin3°…sin89°

=(sin1°sin89°)(sin2°sin88°)…(sin44°sin46°)sin45°

=(sin1°cos1°)(sin2°cos2°)…(sin44°cos44°)sin45°

从而

例2　设x，y，z均为非负数，且满足关系式x=y+z-1=4-y-2z,求u=2x2-2y-z的最值.

解题策略　若将x与y表示为关于z的式子，并代入u得关于z的二次函数，只能求得最小值而无法求得最大值，思维受阻，若将x+y+z作为整体设元，结合题设等式(注意是3个等式)，可获得一种简便的解法.

解：设x+y+z=k，结合原条件，有整体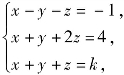解得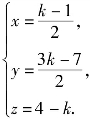

代入u可得

由于x，y，z均为非负数，则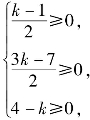解得

当即x=y=z=1时，u最小值=-1；

当k=4,即时，

例3　(1)求棱长为a,各面均为等边三角形的四面体的表面积和体积；

(2)已知四面体ABCD中，AB=CD=8,AC=BD=10,AD=BC=12,求四面体ABCD的体积V.

解题策略　第(1)问，多面体的表面积是各个面的面积之和，求几何体的体积的基本方法有公式法、割补法和等积更换法，把四面体补成一个正方体，使原四面体是由正方体的六条面对角线构成，就是构造整体法的思路，当然由于本例所给的几何体是正四面体，这种方法的优势不明显.第(2)问，实质上是第(1)问的推广，给出的四面体的对棱相等，若用公式法则操作实属不易，割补法也难入手.这时候通过等积变换整体构造法的优势就体现出来了，显然这个四面体是由长方体的6条面对角线构成的，一般地，若四面体的三组对棱长分别为a，b，c，则设长方体的三度为x，y，z,则由可得

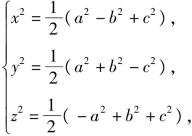则x，y，z的值可求得(必须满足x2>0，y2>0，z2>0)，

代入x，y，z的值即得所求的V.

解：(1)四面体S-ABC(如图10-4所示)的表面积S=4S△ABC,取AB的中点D，联结CD,则于是

对四面体S-ABC的体积V，一般有以下3种解法，其中解法三将四面体补成一个正方体的方法就是运用整体思想的一个范例，实质上，分割与补形是互相转化的两个方面.

图10-4

解法一　(公式法)如图10-4所示，过S作SO⊥平面ABC,联结SD,则在Rt△SOD中，可得

则由锥体的体积公式可得

解法二　(分割法)不难证明AB⊥平面SDC.(www.xing528.com)

又

图10-5

解法三　(补形法)如图10-5所示，将题中正四面体补成一个正方体(正四面体实质上是由正方体的6条面对角线构成)，正方体的棱长为于是所求正四面体的体积

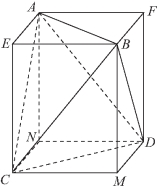
图10-6

(2)可知AB、CD，AC、BD，AD、BC分别是异面直线，故分别过AB，CD作两平行平面，过AC，BD作两平行平面，可得一平行六面体AEBF-NCMD,由AB=CD,可得AEBF对角线相等，故AEBF为矩形；同理，平行六面体的6个面均为矩形，故它是长方体(如图10-6所示).设AF=x,AE=y,AN=z,则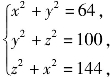

解得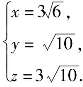

注意：还需要指出的是运用补体法求四面体的体积是有条件的，四面体的每个面是锐角三角形才可能存在3组对棱相等的四面体.

例4　(1)设A(x1,y1)，B(x2,y2)两点在抛物线y=2x2上，直线l是AB的垂直平分线，当直线l的斜率为2时，求l在y轴上截距的取值范围；

(2)已知双曲线经过点M(1，1)能否作一条直线l，使l与双曲线交于点A，B,且点M是线段AB的中点？若存在这样的直线l，求出它的方程；若不存在，说明理由.

解题策略　在解析几何中为了求出某个量或探索存在性问题，常常需要借助其他量，对于这些辅助量，只需表示而不必求出，谓之“设而不求”.比如本例两个小题，都需要设出A(x1,y1)，B(x2,y2)，但这两点的坐标是不需要求出的，而且x1，y1，x2，y2常常构成如等表示，可以将其视作整体结果加入解题过程，这本质上也是一种整体代换，通常用于解决直线与圆锥曲线相交中涉及弦的中点问题.运用“设而不求”,一要注意弦所在直线的斜率是否存在，二要注意运用判别式检验弦所在直线与曲线是否相交.第(1)问的解法中利用了“弦的中点在曲线内部”，对于封闭曲线和抛物线是可以的，但双曲线比较特殊，故第(2)问只能运用判别式讨论直线l的存在与否.

解：(1)设A(x1,y1)，B(x2,y2)两点在抛物线y=2x2上，直线l是AB的垂直平分线，设直线l在y轴上的截距为b,依题意直线l的方程为y=2x+b,又设AB的中点为P(x0,y0)，则有两式相减可得

代入直线方程y=2x+b,得

∵线段AB的中点P(x0,y0)在抛物线(含焦点)的内部，

解得

即直线l在y轴上截距b的取值范围为

(2)设存在被点M平分的弦AB，且A(x1,y1)，B(x2,y2)，

则

①②两式相减，得　　⑤

把③④代入⑤得故直线AB的方程为y-1=2(x-1),

由消去y,得2x2-4x+3=0,而Δ=(-4)2-24=-8<0.

这说明直线AB与双曲线不相交，故被点M平分的弦不存在，即不存在这样的直线l.