整体处理法：提升效率的关键

整体思维就是将问题看成一个完整的整体，把注意力和着眼点放在问题的整体上，全面地收集和获取信息，达到顺利而又简捷地解决问题的目的.

例1　已知f(x)=asin5x+bx3+cx+8(a，b，c为常数)，f(2)=10,求f(-2)的值.

解题策略　所给函数解析式前三项均为奇次幂，最后一项是常数8，显然可以构造g(x)=asin5x+bx3+cx这一奇函数，则g(-x)=-g(x)，g(-2)=-g(2),这种视前三项为一个整体的方法称之为整体处理，而相对于f(x)而言是取了其中的一部分，这也是一种以特殊性处理问题的方法.

解：设asin5x+bx3+cx=g(x),则f(x)=g(x)+8,而g(x)显然是R上的奇函数，故有g(-x)=-g(x)，本题中g(-2)=-g(2).

由f(2)=g(2)+8=10,得g(2)=2,故

f(-2)=g(-2)+8=-g(2)+8=-2+8=6.

例2　已知sinα+3cosα=2,求的值.

解题策略　若用解方程组的方法运算量太大，故可设=k,原问题转化为求k的值.

解：设=k,结合已知式sinα+3cosα=2可得则整理得k2+4k-2=0,解得故

例3　(1)设x，y为实数，若4x2+y2+xy=1,则2x+y的最大值是________；

(2)已知x,y∈R+，满足2x+y=1,则的最小值为(　　).

解题策略　本例两小题若由条件采取消元法转化为一元问题再求其最值，理论上讲得通，但操作不易.第(1)问，由于条件较复杂，消元无法实现；第(2)问，消元虽然易于办到，但得到的是无理式，求其最小值仍然困难很大(当然，运用三角换元可以实现化无理为有理的目标).如果我们注意数学问题中式的结构特征，实行整体换元，则解题思路顿时清晰起来.第(1)问，将2x+y视为一个整体，与题设条件联立，可把问题转化为x的一元二次方程，利用判别式法轻松得到答案；第(2)问，可把看作一个整体，也可把1用2x+y这个整体代入，都能得到极其巧妙的解法.

解：(1)令2x+y=t,则y=t-2x,代入4x2+y2+xy=1中，得6x2-3tx+t2-1=0,将它看作一个关于x的二次方程，t为参数，则由其判别式大于等于0，可得Δ=(3t)2-4×6×(t2-1)≥0,解得的最大值是

(2)解法一　(以为整体，转化为求t的最小值)

令移项得则(x-t)2=x2+y2,

由得y2-ty+t-t2=0，此方程有解的必要条件是Δ≥0,

即t2-4(t-t2)≥0,解得t≤0或

而又当时，得符合题意.

取最小值故选A.

解法二　(设视2x+y为整体，构造新元运用判别式法求解)

由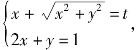得即

两边平方并整理得4t(t-1)x2+2t(2t-1)xy+(t2-1)y2=0,

即

Δ=4t2(2t-1)2-4×4t(t-1)(t2-1)=4t(5t-4)≥0,注意到

又当时，结合2x+y=1，得当且仅当时，取最小值故选A.

解法三　(构造以为新元的函数，换元并利用三角函数有界性求解)

∵2x+y=1,x>0,y>0.(www.xing528.com)

令则

记则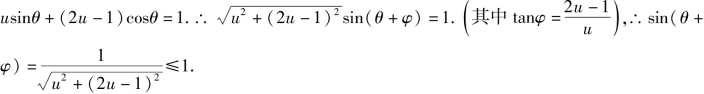

∴u2+(2u-1)2≥1,整理得

当时，

结合2x+y=1，得当且仅当时，取最小值故选A.

例4　(1)过圆O：x2+y2=10外一点P(3，4)向圆O作两条切线，切点分别为A，B，求直线AB的方程，并对此命题进行推广；

(2)过圆x2+y2=R2内部一点M(a,b)作动弦AB,过A，B分别作圆的切线，设两条切线的交点为P，求证：点P恒在一条定直线上运动.

解题策略　第(1)问，已知圆方程x2+y2=R2及圆上一点A(x1,y1),则过点A且与圆x2+y2=R2相切的方程是x1x+y1y=R2,若圆上另一点B(x2,y2),则过点B且与圆x2+y2=R2相切的方程是x2x+y2y=R2，而本题要求的是直线AB的方程，如果说上述两条切线相交于P(m,n)，则此点必同时满足两条切线方程，就可得mx1+ny1=R2,mx2+ny2=R2,从而说明了A(x1,y1)及点B(x2,y2)均在直线mx+ny=R2上，这就是圆的切点弦AB的方程.上述解题思路就是典型的整体处理法，有效地避开了大量复杂的运算，按照这种整体处理法我们不仅可将圆推广到更为一般的情形，还可以得到椭圆、双曲线及抛物线切点弦的方程.第(2)问，求证圆内部一点作动弦AB，过A，B分别作圆的切线且两切线交点为P，则点P恒在一定直线上运动，其证法仍然是整体处理法，同时也说明了题中的点所担任的运动与静止的角色是相对的，同一个点，根据需要，可随时灵活选择和变换其角色，常得妙解.

解：(1)设切点A(x1,y1)，B(x2,y2)，则过点A，B的圆x2+y2=10的切线方程分别为x1x+y1y=10,x2x+y2y=10.

又∵两切线均过点P(3,4)，故有3x1+4y1=10,3x2+4y2=10.

这就说明点A(x1,y1)及点B(x2,y2)均在直线3x+4y=10上.

不同两点决定唯一的直线，∴直线AB的方程为3x+4y=10.

按照上述整体处理法，可得下面一系列推广性命题：

推广一　过圆(x-a)2+(y-b)2=R2外一点P(m,n)向圆作两条切线，切点分别为A，B,则切点弦AB所在的直线方程为

(m-a)(x-a)+(n-b)(y-b)=R2.

推广二　过椭圆外一点P(m,n)向椭圆作两条切线，切点分别为A，B,则切点弦AB所在的直线方程为

推广三　过双曲线外一点P(m,n)向双曲线作两条切线，切点分别为A，B,则切点弦AB所在的直线方程为

推广四　过抛物线y2=2px(p>0)外一点P(m,n)向抛物线作两条切线，切点分别为A，B,则切点弦AB所在的直线方程为

ny=p(x+m).

(2)设A(x1,y1)，B(x2,y2)，P(x0,y0)，不妨将A，B，P都视为定点(视动为静)，先求直线AB的方程.

切线PA的方程为x1x+y1y=R2,切线PB的方程为x2x+y2y=R2,

∵P点在切线上，∴x1x0+y1y0=R2,x2x0+y2y0=R2.

这表明点A，B都在直线x0x+y0y=R2上，故直线AB的方程为

x0x+y0y=R2,

又∵点M在直线AB上，∴x0a+y0b=R2　　①

对任意点P(x0,y0)都满足式①，故动点P必在直线ax+by=R2上(换静为动).