整体代换法：完善大规模最优化

在解题过程中，将已知某个部分整体代入达到简化运算、迅速使原问题获解的方法称之为整体代换法.

例1　若正数x，y满足x+3y=5xy,则3x+4y的最小值是(　　).

解题策略　在解题过程中，将已知某个部分整体代入可简化运算.比如本例条件x+3y=5xy可变形为即把1用代换；这是一种常值代换，若设t=3x+4y代入x+3y=5xy,则为整体代换，可使原问题转化为求t的最小值.

解法一　(将已知条件进行转化，通过常值代换，再利用基本不等式求解)

∵x>0,y>0，由x+3y=5xy得

∴3x+4y

(当且仅当x=2y时取等号)

∴3x+4y的最小值为5，故选C.

解法二　(整体代换)设t=3x+4y,

由得20y2+5(1-t)y+t=0　　①

∵y>0,∴方程①有两个正根，故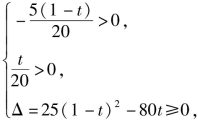解得t≥5.

∴3x+4y的最小值为5，故选C.

例2　已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1.

(1)求椭圆C的标准方程；

(2)若直线l:y=kx+m与椭圆C相交于A，B两点(A，B不是左右顶点)，且以AB为直径的圆过椭圆C的右顶点，求证：直线l过定点，并求出该定点的坐标.

解题策略　设A(x1,y1)，B(x2,y2)，以AB为直径的圆过椭圆C的右顶点，则必定有斜率之积为-1这个关系式，从而出现用x1+x2，x1x2，y1+y2，y1y2表示的等式，联立直线l与椭圆C的方程通过消元并运用韦达定理可得x1+x2，x1x2，y1+y2，y1y2用参数m，k表示的关系式，通过整体代入进行求解.这种“设而不求”是处理解析几何问题最基本的思路，解题过程简捷，计算量小，实质上是利用问题中整体与局部的关系，通过整体代入、整体运算、整体消元等方法简化运算过程，顺利求解.

解：(1)设椭圆的标准方程为

∴a=2,c=1,b2=3,因此，椭圆C的标准方程为

(2)设A(x1,y1),B(x2,y2),由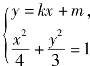得(3+4k2)x2+8mkx+4(m2-3)=0,(www.xing528.com)

则Δ=64m2k2-16(3+4k2)(m2-3)>0,3+4k2-m2>0.

由韦达定理得

∵以AB为直径的圆过椭圆的右顶点D(2,0),故kAD·kBD=-1.

整理得y1y2+x1x2-2(x1+x2)+4=0.

代入得化简得7m2+16mk+4k2=0,由此解得且满足3+4k2-m2>0.

当m=-2k时，l:y=k(x-2),直线过定点(2,0)，而(2,0)为右顶点，与已知矛盾；

当时，直线过定点

综上可知，直线l过定点，定点坐标为

例3　对任意n∈N*,求证:

解题策略　不等式左边是n个因式的连乘积，直接证明肯定困难，解题关键是对不等式左边部分的结构特点有清晰的认识.

若设

显然an是代数式中的一部分.这个代数式就是整体，而an是它的局部，我们再构造两个相关式

显然bn，cn也是上述代数式的局部，即上述代数式=an·bn·cn,利用这种整体与局部的关系，结合放缩法可顺利获证.

证明　设

构造相关式

故

从而