整体与局部关系的优化探讨

事物的发展变化本来就是一个整体和系统，故观察事物必须着眼于整体和系统，运用整体观来处理问题，同时事物的发展变化，必然会凸显某些关键的部分，而对这“部分”的结构特征和变化特点或趋势作深入分析，往往能体现出事物整体结构特征及其变化发展的趋势甚至规律，这就启发我们在分析解决数学问题时既要着眼于整体又必须关注局部，就是通常讲的从整体着眼，从局部入手，得出初步结论后，再进一步研究.一个较为复杂的数学问题，有时局部处理得当有助于整体的解决，局部处理又可分为局部解决、局部固定和局部调整3种类型.

例1　已知正三棱锥P-ABC的高为其内部有一个球与它的4个面都相切，求：

(1)正三棱锥P-ABC的表面积；

(2)正三棱锥P-ABC内切球的表面积与体积.

解题策略　思考下列启发式问题：

(1)要求正三棱锥内切球的表面积与体积，公式S球=4πR2与中需要求出哪些量？

(2)上一问，显然只要求出球的半径R即可，那么半径R与三棱锥的各棱长或者各个面有什么联系？这些互相联系的数量如何求出来？

(3)如果用等体积法求解，那么如何对三棱锥这个整体进行适当分割，即如何实现整体与局部之间的转化呢？

图10-1

解：(1)如图10-1所示，底面三角形中心O到AC的距离

则正三棱锥侧面的斜高为

∴S侧

故S全=S侧+S底

(2)设正三棱锥P-ABC的内切球球心为O1,联结O1P，O1A，O1B，O1C,而点O1到三棱锥的4个面的距离都为球的半径r.

∴VP-ABC

又

解得

∴

例2　四面体的6条棱中，有5条棱长都等于a.

(1)求该四面体体积的最大值；

(2)当四面体的体积最大时，求其表面积.(www.xing528.com)

解题策略　从整体上求四面体体积，可运用公式但这个h比较难求，故可寻找四面体的直截面(与侧棱垂直且过一条底边的截面)，把这个整体分割为两个锥体求体积，再求和，这是一种通解通法.由于本例涉及最值问题，一般思路是在得到解析式后利用函数思想或基本不等式进行求解.

解：(1)如图10-2所示，在四面体A-BCD中，设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P，BC的中点为E，联结BP，EP，CP,由AD⊥平面BPC可得

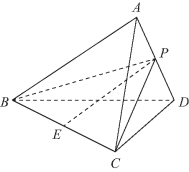
图10-2

VA-BCD

当且仅当时，VA-BCD的最大值为

(2)由(1)知S表

图10-3

例3　如图10-3所示，已知点D为Rt△ABC斜边BC上一点，且AB=AD,记∠CAD=α，∠ABC=β.

(1)证明：sinα+cos2β=0.

(2)若求β的值.

解题策略　证明sinα+cos2β=0,即把sinα+cos2β看作一个整体，求出它的值为0，另外，在解三角形问题时，必须抓住三内角之和为π这一整体.

解：(1)∵AB=AD,∴∠ABD=∠ADB=β,∠BAD=π-2β,

即

即sinα+cos2β=0.

(2)在△ADC中，由正弦定理得

令t=sinβ,则解得(舍去).