运用特殊和一般的辩证关系优化解题方法

“一般”概括了“特殊”，“一般”比“特殊”更能反映事物的本质，因此人们常常把许许多多特殊具体的事物置于一般的普遍的事物中，通过对一般情形的讨论、转换去解决和处理特殊的问题，事物的特殊性中包含着普遍性，即所谓共性存在于个性之中，相对于“一般”而言，特殊的事物往往更简单、直观、具体,更容易认识，因而在处理一般性问题时，常常从特殊的情况入手，通过对特殊情况的研究，找出处理“一般”问题的方案，使“一般”的问题得到解决，这就是特殊化的解题策略.特殊化常表现为范围的收缩或限制，即从较大范围的问题向较小范围的问题过渡，或从某类问题向其子类问题的过渡.显然，较为理想化的特殊问题是其自身容易解决的，且从其解决过程中又易发现或得到一般性问题的解法，所以，特殊化策略的关键是能否找到一个最佳的、“一针见血”的特例.

例1　设f(x)=1-acosx-bsinx-Acos2x-Bsin2x,其中a，b，A，B均为常数，如果f(x)≥0对所有实数x都成立，求证：a2+b2≤2且A2+B2≤1.

解题策略　所给的三角函数解析式非常复杂，且有四个字母参数a，b，A，B，如何把这些字母参数从解析式中剥离出来呢？利用“特殊探路”处理不等式相关问题是上策，抓住不等式f(x)≥0对所有实数x都成立，可将x换成特殊值(可以是多次)，把a，b或A，B剥离出来，这也是“以退求进”的解题策略.

证明　将f(x)变形：　　①

将①中的x换成则

　　②

①+②，得：

即对任意x∈R,有　　③

取x的特殊值代入③,得即a2+b2≤2.

将x代之以变量x+π,由①得

　　④

①+④，得　　⑤

因为⑤对任意x∈R都成立，故对特殊值也成立，从而，得：即A2+B2≤1.

图9-3

例2　如图9-3所示，椭圆的左焦点为F1，右焦点为F2,离心率过点F1的直线交椭圆于A，B两点，且△ABF2的周长为8.

(1)求椭圆E的方程；

(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q，试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由.

解题策略　本例第(2)问用一般情况解还是用特殊探路的方法解，很值得比较.若通过一般情况解，即直接假设点P存在，依据条件得出点P的坐标，但在动直线y=kx+m上有两个参变量的前提下进行推理运算，明显需要较强的技巧，下面给出的两种解法，读者一定会感觉非常烦琐；若通过特殊探路(由椭圆的对称性，其特殊性还是容易找到的)的方式求解，猜测一般问题的结果，再给予证明，显得自然、简捷，由此有了第三种解法，这里，特殊化解题的好处得到了一定的体现.

解：(1)因为|AB|+|AF2|+|BF2|=8,即|AF1|+|F1B|+|AF2|+|BF2|=8,

又|AF1|+|AF2|=|BF1|+|BF2|=2a,所以4a=8,得a=2.

又因为即所以c=1,所以

故椭圆E的方程是

(2)由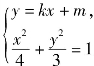得(4k2+3)x2+8kmx+4m2-12=0.

因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,

即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0　　①

此时所以

由得Q(4,4k+m).

探究点M的存在性，有如下几种解法.

解法一　假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上，设M(x1,0),则对满足①式的m,k恒成立.

因为

由得

整理得　　②

由于②式对满足①式的m,k恒成立，

所以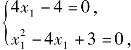解得x1=1.

故存在定点M(1,0)，使得以PQ为直径的圆恒过点M.

解法二　以PQ为直径的圆中，圆心为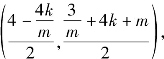

半径

所以圆方程为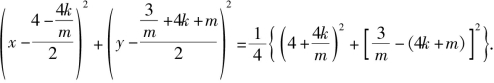

令y=0,得

所以x=1或所以存在点M(1,0)，使得以PQ为直径的圆恒过点M.

解法三　假设平面内存在定点M满足条件，由图形对称性知，点M必在x轴上，取此时(此时运用特殊化法).

以PQ为直径的圆为交x轴于点M1(1,0),M2(3,0);

取此时(取另一组特殊值)，

以PQ为直径的圆为交x轴于点M3(1，0)，M4(4,0),

所以若符合条件的点M存在，则点M的坐标必为(1,0).

以下证明M(1,0)就是满足条件的点(通过上面特殊探路，猜测一般问题的结果，再给予证明)：

因为点M的坐标为(1,0)，所以从而故恒有即存在定点M(1，0)，使得以PQ为直径的圆恒过点M.

例3　在数列{an}与{bn}中，a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项，n∈N*.

(1)求a2,b2的值；

(2)求数列{an}与{bn}的通项公式；

(3)设Tn=(-1)a1b1+(-1)a2b2+…+(-1)anbn,n∈N*，证明：|Tn|<2n2,n≥3.

解题策略　第(1)问，只需由一般到特殊演绎计算，而第(2)、第(3)两问，则要由特殊到一般的归纳探索，其中第(2)问，关键是探索得到数列{an}的通项可以有不同的方法.第(3)问，关键是计算Tn,其中涉及(-1)a1,(-1)a2,…,(-1)an,故对an是奇数还是偶数必须分类讨论，由此得到(-1)anbn的分段表示，再由此得出Tn的分类计算结果.在解决了关键问题之后，证明|Tn|<2n2(n≥3)就不难了.通过对这道题的分析，我们发现运用特殊与一般的辩证关系可以优化解题过程.

解：(1)(特殊化与一般化，分类与归纳，解方程求a2,b2)(www.xing528.com)

由已知递推关系，可知S2-4S1=0，(特殊化)

即a1+a2-4a1=0,解得a2=3a1=3，

由已知可知，(2a2)2=b1·b2,则

(2)❶首先探索数列{an}的通项，有三种方法：

方法一　由已知，可知(这是一般式，再特殊化)

则有

等式两边分别相乘，左边(有限项相乘，由特殊到一般)

右边(相约后分子、分母各剩3个因式)

所以，(前n+1项之和)，

那么，an+1

所以，数列{an}的通项为

方法二　由已知nSn+1-(n+3)Sn=0移项得n(Sn+1-Sn)=3·Sn，

则nan+1=3·Sn,当n≥2时，(n-1)an=3·Sn-1，

两式相减，得n·an+1-(n-1)an=3an,整理为(这是一般式，再特殊化)

则有

等式两边分别相乘，得(用累乘法，n=1时也成立)

所以

方法三　由a1=1,即S1=1，代入nSn+1-(n+3)Sn=0,依次计算，得a2=3,a3=6,a4=10.

依次求差，a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n，

等式两边分别相加，得an-a1=2+3+4+…+n，

可知

❷探索数列{bn}的通项，由上述任何一种方法求得后继续解下去：

又由已知，可知(2an+1)2=bn·bn+1,即

所以，(再特殊化依次推理)

则有

依次类推，(类比推理所得的结果)

所以，数列{bn}的通项为bn=(n+1)2(n∈N*).

(3)证明　由(2)知，

注意到的奇偶特征，为

因而设n=4k(k=1,2,…)，

则(-1)an·bn

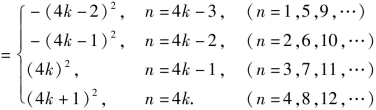
所以T4k=(-22-32+42+52)+(-62-72+82+92)+…+[-(4k-2)2-(4k-1)2+(4k)2+(4k+1)2].

设ck=-(4k-2)2-(4k-1)2+(4k)2+(4k+1)2=(8k-1)×1+(8k-1)×3

=32k-4

=28+(k-1)×32(等差数列通项ck=c1+(k-1)d),

则数列{ck}是首项c1=-22-32+42+52=28,公差d=32的等差数列.

而T4k+1=T4k+(-1)a4k+1·b4k+1=16k2+12k-(4k+2)2=-4k-4,

T4k+2=T4k+1+(-1)a4k+2·b4k+2=-4k-4-(4k+3)2=-16k2-28k-13,

T4k+3=T4k+2+(-1)a4k+3·b4k+3=-16k2-28k-13+(4k+4)2=4k+3,

当n≥3时，k≥1,

此时，T4k>0,T4k+1<0,T4k+2<0,T4k+3>0.

那么当n=4k时，即n=4,8,12,…,4k,…

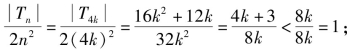
当n=4k+1时，即n=5,9,13,…,4k+1,…

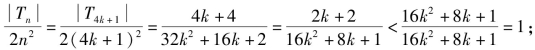
当n=4k+2时，即n=6,10,14,…,4k+2,…

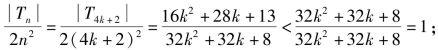
当n=4k+3时，即n=7,11,15,…,4k+3,…

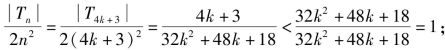
又当n=3时，

综上所证，对n∈N*且n≥3,总有即|Tn|<2n2成立.