特殊化法解答填空和选择题最佳方法

一般成立，其特殊也成立；特殊不成立，其一般也不成立.依据这一逻辑思维原理，当填空、选择题的结论唯一或其值为定值时，可把题中参变量用特殊值(或特殊函数、特殊点、特殊角、特殊数列、特殊图形位置、特殊方程、特殊模型)代替之，则可得结论，往往解题速度快、效果好、正确率高.特殊化法是一种以退为进的方法，在解答具有一般性的数学问题时，直接推进有困难或无路可“进”，不妨从一般性的问题退到特殊性的问题上来，利用问题在某一特殊情况下不真，则它在一般情况下也不真的原理获得结果或选项.

例1　(1)在△ABC中，角A，B，C所对的边分别为a，b，c，若a，b，c成等差数列，则________.

(2)函数的值域是(　　).

(3)函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则(　　).

A.f(x)是偶函数　　　B.f(x)是奇函数

C.f(x)=f(x+2)　　　D.f(x+3)是奇函数

解题策略　当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值或是一个确定的范围、或具有某种确定的性质时，可以把题中变化的不定量用特殊值代替，即可以得到正确结果.第(1)问采用特殊化法，用符合题设的特殊三角形确定所求值；第(2)问，给出的四个选项中有真包含关系，可考虑用特殊值法排除不可能选项；第(3)问，同样运用特殊化法即选择一个特殊的最为基本的函数排除不可能选项.

解：(1)令a=3,b=4,c=5,则△ABC为直角三角形，从而所求值为

(2)令sinx=0，cosx=1,则淘汰A.

令得当sinx=-1时，矛盾，淘汰C，D，故选B.

(3)令f(x)=sinπx,则f(x+1)=sinπ(x+1)=-sinπx,f(x-1)=sinπ(x-1)=-sinπx，可知，当f(x+1),f(x-1)都是奇函数时，f(x)不是偶函数，淘汰A.

令则且

可知，当f(x+1),f(x-1)都是奇函数时，f(x)不是奇函数，且f(x)≠f(x+2),淘汰B，C,故选D.

在上述的分析中用两个f(x+1)，f(x-1)都是特殊奇函数，否定选项A，B，C,从而选D.

事实上，f(x+1)是奇函数，则f(x)=f(x-1+1)=-f[-(x-1)+1]=-f(-x+2)；f(x-1)是奇函数，则-f(-x+2)=-f[(-x+3)-1]=f(x-3-1)=f(x-4),

∴f(x)=f(x-4).

那么f(x+3)=f(x+3-4)=f(x-1)是奇函数，因而知选D.

例2　(1)已知和的夹角为45°，且则________.

(2)在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则

A.2　　　B.4　　　C.5　　　D.10

(3)已知二面角α-l-β为60°，动点P，Q分别在面α,β内，P到面β的距离为到面α的距离为则P，Q两点之间距离的最小值为(　　).

解题策略　第(1)问，把图形放在平面直角坐标系中，容易得出结果；第(2)问，运用特殊图形法；第(3)问，运用特殊位置法，把P,Q的一般位置转化为在二面角的一个平面角的两边上计算.

解：(1)依题意可设其中t>0,再由得(t-2)2+t2=10,进而解得t=3,

故

(2)选取等腰直角三角形ABC,以直角顶点C为原点，CA所在直线为x轴，CB所在直线为y轴建立平面直角坐标系，并设A(4,0)，B(0,4),则得D(2,2),P(1,1),进而得故选D.

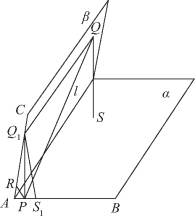
图9-2

(3)(当点P，Q分别在二面角的一个平面角的两边时，P，Q之间的距离最小)设过点P的二面角的平面角为∠BAC=60°,过点Q在β平面内作QQ1∥l交AC于Q1，

则QQ1∥平面α，点Q到平面α的距离分别是点Q1,Q在α内的射影，如图9-2所示，且QQ1⊥平面BAC,联结PQ，PQ1,则QQ1⊥Q1P,所以PQ>PQ1(斜边大于直角边).(www.xing528.com)

由得AS1=2,AQ1=4.

由得AR=1,AP=2.

在△Q1AP中，所以当点Q与Q1重合时取等号，故选C.

例3　(1)如果奇函数f(x)在[3,7]上是增函数且最小值为5，那么f(x)在区间[-7,-3]上是(　　).

A.增函数且最小值为-5　　　B.减函数且最小值为-5

C.增函数且最大值为-5　　　D.减函数且最大值为-5

(2)在等差数列{an}中，am=n,an=m,则am+n=(　　).

A.0　　　B.m　　　C.n　　　D.m+n

(3)已知与均为单位向量，其夹角为θ,有下列4个命题：

其中的真命题是(　　).

A.P1，P4　　　B.P1，P3　　　C.P2，P3　　　D.P2，P4

解题策略　第(1)问，构造符合条件的特殊函数求解；第(2)问，构造符合条件的等差数列，运用排除法；第(3)问，取两向量夹角中的特殊角，向量夹角范围是[0,π]，从选择点上看，显然0和π是特殊角.

解：(1)构造特殊函数显然满足题设条件，并易知f(x)在区间[-7,-3]上是增函数，且最大值为f(-3)=-5,故选C.

(2)构造等差数列{an}使得a1=2,a2=1,这里m=1,n=2,于是am+n=a3=0,排除B，C，D,故选A.

(3)(取特殊角法)本题中4个命题都以可逆的形式给出，因此判断时大可不必再考虑可逆性，依据4个命题的关系和特征将其分成两组进行判断，对于命题P1，P2,只需取θ=0或θ=π，即可判断命题P1为真；对于命题P3，P4,也只需取角θ=0或θ=π,即可判断出命题P4为真，故选A.

例4　(1)已知双曲线b2x2-a2y2=a2b2(a>b>0)的渐近线夹角为α,离心率为e,则等于(　　).

(2)已知a，b为异面直线，P为空间的一点，则过P且与a，b成60°角的直线有(　　).

A.3条　　　B.2条或3条

C.3条或4条　　　D.2条或3条或4条

(3)正四棱锥相邻侧面所成二面角的平面角为α,侧面与底面所成二面角的平面角为β,则2cosα+cos2β的值为(　　).

A.1　　　B.0.5　　　C.0　　　D.-1

解题策略　第(1)问，原双曲线即为从中选择特殊的容易计算的双曲线，通过计算，容易求解结果；第(2)问，进行类比试验求解；第(3)问，抓住当正四棱锥的高充分大时角α，β的变化，进行推断.

解：(1)条件中给出的双曲线即为形式，取符合条件的特殊双曲线如易得离心率故选C.

(2)当a，b所成角小于60°时，显然有2条；当a，b所成角等于60°时，可知有3条；当a，b所成角大于60°且小于90°时，不难得知有4条，故选D.

(3)显然α为钝角，当棱锥的高充分大时，可有β>45°,从而2β>90°,由此可得2cosα+cos2β<0,故选D.