由特殊到一般的归纳与一般到特殊的演绎,是两种非常重要的思维方法,是人们认识事物的两个对立而又统一的过程,关于一般化和特殊化,大数学家希尔伯特给出了下面的精彩论述:
“在解决一个数学问题时,如果我们没有获得成功,原因常常在于我们没有认识到更一般的观点,即眼下要解决的问题不过是一连串有关问题中的一个环节,采用这样的观点以后,不仅我们研究的问题会容易得到解决,同时还会获得一种能应用于有关问题的普遍方法.”
“在讨论数学问题时,我们相信特殊化比一般化起着更为重要的作用,可能在大多数场合,我们寻求一个问题的答案而未能成功的原因是:有一些比手头的问题更简单、更容易的问题还没有完全解决或完全没有解决,这时,一切都有赖于找出这些比较容易的问题,并使用尽可能完善的方法和能够推广的概念来解决它们.”
这里,希尔伯特提出了“特殊化”与“一般化”的解题策略.
命题的一般结论可以从特殊情况中反映出来,而特殊情况往往是更具体化、简单化,从而易于入手,发现解题规律,特殊化是把研究对象或问题从原有范围缩小到较小范围或个别情形进行考察的思维方法,由于一般性总是寓于特殊性之中,所以要研究某一对象或问题时,就可以先考察它的若干个特殊情形,利用各个特殊情形中包含着的共性和个性,通过比较、归纳、分析和综合来把握原有对象或问题的有关性质.(https://www.xing528.com)
将一般问题特殊化的解题框图如图9-1所示.
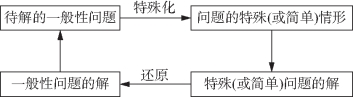
图9-1 将一般问题特殊化的解题框图
正如希尔伯特指出的“在讨论数学问题时,我相信特殊化比一般化起着更为重要的作用”,G.波利亚则把特殊化称为“获得发现的伟大源泉”.
当然,通过对一般性命题的研究解决特殊的命题是解题的另一策略.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




