解题中的互变思想优化指南

矛盾着的东西往往也都互相联系着，不但可以在一定条件下共处于一个统一体中，而且可以在一定条件下互相转变，如“熟悉”与“陌生”，“合”与“分”，“正”与“逆”，“动”与“静”，“进”与“退”，“一般”与“特殊”，“强化”与“弱化”，“抽象”与“具体”，“直”与“曲”，“主”与“次”，“整体”与“部分”，“有限”与“无限”，“或然”与“必然”等.一个事物矛盾的两个方面，既是对立又是统一的，更是可以相互转换的，从哲学上讲既是“一分为二”，又是“合二为一”，互变是化归的一种手段，但比化归更深刻，哲学的意味更浓，当今学术界倡导的批判性思维，在数学上的体现就是“互变”，就是对立又统一的辩证思想.

关于互变思想在解题中的运用，本书各章都有涉及，在“转化与变换的思想”这一章中已有多个专题进行论述.本章及本专题对此稍加拓展，可以这样来表述：互变思想是指在处理、解决数学问题的过程中有意识地考虑对问题进行相互变化，从彼此相反的状态、形式中寻找相互变化的途径.

例1　在实数集内解方程：

解题策略　本题是一个四次方程，且系数含无理数，用通常的方法不易求解，但如果把视为主元，把x视为参数，由可得以为主元的二次方程，解之就简单了，这种题中元素之间角色的互换为某些看似难以解答的问题开辟了一条通道.

解：原方程变为

解上述关于的二次方程得：

于是，

例2　在坐标平面xOy上有一运动着的梯形梯形在OA+OB=4的条件下运动，求原点O到直线CD的最短距离.

解题策略　相对于原点O,梯形是在运动的，直线CD是动直线，很难表示，若“动”与“静”互换角式，将梯形看作是静止的，则原点O是运动的，A，B就成为两个定点，则O的轨迹可求，CD也就成为定直线了，解题思路在角色的“动”“静”互变中产生了.

解：因为梯形是运动的，所以动直线的方程难以表示，即使求得，也必含参数且比较复杂.若将梯形看作静止而原点O是运动的，则由可知，动点O的轨迹是以A，B为焦点的椭圆.建立以AB中点O′为“原点”，AB中垂线为x′轴的新坐标交x′O′y′，则直线CD的方程为：动点O的轨迹方程为设O在新坐标x′O′y′下的坐标为O(cosθ，2sinθ)，则O到直线CD的距离为

当且仅当sin(θ+φ)=1时，原点O到直线CD的最短距离为

例3　在△ABC中，求证：

解题策略　三角形中三角不等式的证明是个难点，运用放缩的技巧是必然的，问题在于如何进行适当的放缩，如果把A，B两角视为整体变形，则C如何处理？总要为C配套另一个角，这个角必须与三角形内角相关，容易想到引进这个角.这样我们可以试试加上三角形三内角和的平均值的正弦来证.

证明　

又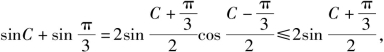

例4　已知函数y=f(x)满足：且当n∈N*时，如果存在正项数列{an}满足条件：

(1)求数列{an}的通项公式；(www.xing528.com)

(2)求证：

(3)求证：

解题策略　第(1)问，由条件求得递推关系后运用累乘法是求数列通项公式的一种常用方法.第(2)、第(3)两问是数列不等式的证明，一般对于分母是两个或多个相继整数积的倒数和小于某常数的不等式的证明，通常对不等式左边用放缩裂项法，适当放缩使之能够裂项相消.这里面放缩的技巧很重要，而通分与裂项又正是相反的两种变形手段.

解：(1)　　①

　　②

由①②得a1+a2+a3+…+an=n2an　　③

从而a1+a2+…+an-1=(n-1)2an-1　　④

④式代入③式得(n-1)2an-1+an=n2an，由此可得

∴an

(2)由(1)得，当i>2时，有

(3)关键是如何进行裂项.

若能出现的模型就好了.

我们进行逆向变形，即从出发变形，

显然有

故要也就是要成立，而此式显然成立.这就是说，所证式从第2项起每一项均可裂成递归的两项之差.于是，有