同向化归解题法：优化技巧详解

同向化归就是把面临的新问题进行命题分割或命题分解，化归为某一(或几)个可简捷处理的子问题，解决了这一(或几)个子问题，从而也就解决了所有子问题，或在推演中，进行同理推导同解变形化简等，这种化归是在同一层次上“平行”转化.

例1　已知数列{an}，{bn}都是公差为1的等差数列，其首项分别为a1，b1，且a1+b1=5，a1，b1∈N*，设cn=abn(n∈N*)，求数列{cn}的前10项和.

解题策略　当我们接触的问题存在着大量可能的答案(或中间过程)，而暂时又无法用逻辑方法排除时，我们只能对每一种可能的情况逐个加以讨论，解决了这些子问题，原来的命题也就完全解决了，本例中由条件可知a1，b1的取值有多种情况，必须对每种情况进行研究，才能得到原问题的最后结果.

解：由题设a1+b1=5，a1、b1∈N*，可将适合条件的可能情况一一列举出来，一共有4种情况：下面逐一求解.

子问题(1)：当a1=1，b1=4时，an=n，bn=n+3，cn=an+3.

子问题(2)：当a1=2，b1=3时，an=n+1，bn=n+2，cn=an+2.

子问题(3)：当a1=3，b1=2时，an=n+2，bn=n+1，cn=an+1.

子问题(4)：当a1=4，b1=1时，an=n+3，bn=n，cn=an.

因此，无论哪种情况，均得到数列{cn}的前10项和为85.

例2　设f(x)=x2-x+k，若log2f(a)=2，f(log2a)=k(a≠1，a>0)，

求使得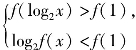成立的x的取值范围.

解题策略　本题结构较为复杂，初看似乎难以下手去做，若根据同向化归解题法，把原问题分解为几个基本的子问题，然后逐个解决，所有的子问题全部解决了，整个大问题也就获解了.由题意，原问题可以分解为如下4个子问题：

子问题1：由方程f(log2a)=k，求a的值；

子问题2：由方程log2f(a)=2，求k的值；

子问题3：求f(1)的值；

子问题4：解不等式组求x的取值范围.

解：按上述子问题的顺序逐一解答.

子问题1：由

∵a≠0，a≠1，∴log2a≠0，∴log2a-1=0log2a=1a=2.(www.xing528.com)

子问题2：由log2f(a)=2log2(a2-a+k)=2.

∴a2-a+k=4，把a=2代入得：k=2.

子问题3：f(1)=12-1+k=2.

子问题4：由上述所求各值，原不等式可化为：

此即为x的取值范围.

例3　一个小于400的3位数，它是平方数，它的前两个数字组成的两位数还是平方数，其个位数也是一个平方数，求这个3位数.

解题策略　可采用同向化归解题法和枚举与筛选并用的策略，即依据题中限定的三个条件步步深入，面对枚举出的情况逐步排除不符合条件的三位数，确定满足条件的三位数.

解：本题共提出3个条件：

(1)一个小于400的三位数是平方数；

(2)这个三位数的前两位数字组成的两位数还是平方数；

(3)这个三位数的个位数也是一个平方数.

先找出满足第一个条件的三位数：

100,121,144,169,196,225,256,289,324,361.

再考虑第二个条件，从中选出符合条件者：169,256,361.

最后考虑第三个条件，排除不符合条件的256，于是找到答案是169和361.

例4　设集合A={x|1<x<3}，又设集合B是关于x的不等式组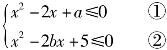的解集，且A⊆B，试确定a，b的取值范围.

解题策略　若设集合B1是不等式①的解集，集合B2是不等式②的解集，则B=B1∩B2，由于两个不等式都含参数，求B1∩B2并非易事，既要分类讨论又极易出错，如果运用同向化归，则简捷多了！根据题设A⊆B⟺A⊆B1且A⊆B2.两个参数“分而治之”，清清楚楚！

解：若记f(x)=x2-2x+a,B1为不等式①的解集；记g(x)=x2-2bx+5，B2为不等式②的解集，则B=B1∩B2.于是A⊆B⟺A⊆B1且A⊆B2.结合图像易得且且b≥3.