横向化归解题法详解及优化技巧

横向化归就是通过对命题的有关量进行转换，各学科知识间的转换，等价变换命题，运用同构变换等手段将生疏、复杂、困难的问题转化为熟悉、简单的问题来处理.

例1　设a，b∈R且方程x4+ax3+bx2+ax+1=0至少有一个实数解，试求a2+b2的最小值.

解题策略　本例是一个有实数解的高次方程，求方程系数构成的代数式a2+b2的最小值.从方程角度去解是困难的，但是我们分析方程系数的特点，发现其具有对称性，且a，b又都是一次的，如果把它看成是a，b的方程，显然是一条直线的方程；如果设a2+b2=r2，可看成点(a，b)在圆上，则原命题等价变换成直线与圆的位置关系问题，即求直线与圆至少有一个公共点时，半径平方的最小值.这就是运用同构变换等手段将复杂的高次方程问题化归为熟悉、容易处理的直线与圆的位置关系问题.

解：因方程至少有一个实数解，不妨设为m≠0，代入得

设a2+b2=r2，构造直线圆C:a2+b2=r2.

则两者之间必有公共点(a，b)，因此圆心到直线的距离小于或等于半径，

即

图8-5

所以即a2+b2的最小值为当且仅当m=±1时a2+b2取得最小值

例2　如图8-5所示，∠MON=60°，边长为a的正三角形ABP在∠MON内滑动(不能翻转)，使得A点始终在OM上，B点始终在ON上，求P点的轨迹方程.

解题策略　本例中A点在射线OM上移动，B点在射线ON上移动，求正三角形另一个顶点P的轨迹方程，常用的求轨迹方程的基本方法如直接法、转移法、参数法很难用上，定义法则根本不相关.对于这类与旋转有关的轨迹问题，采用复数方法来处理具有方便、直观、简捷的优点，因为复数的向量表示把代数与几何融为一体，复数的乘法运算反映在几何上正好是向量的旋转.这种横向化归命题实质上也是同构变换.

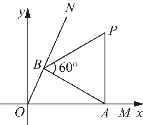
图8-6

解：如图8-6所示，以O为原点，OM所在直线为x轴建立复平面.

设A，B，P3点对应的复数分别为

则

又可由逆时针旋转60°而得到.

(www.xing528.com)

即

又即

将①②代入，整理得：

故P点的轨迹方程为在∠MON内的部分.

例3　在平面直角坐标系xOy中，设P(x，y)是椭圆上的一个动点，求S=x+y的最大值.

解题策略　本例思考方法不同导致形成求解过程的多样性，可以横向化归转化为由方程组有解求S的最大值，可以利用椭圆的参数方程横向化归为求三角函数的最大值，也可以纵向化归，通过坐标变换讨论圆与直线有公共点时求S的最大值.

解法一　由方程组消去x后整理得方程4y2-2Sy+S2-3=0　　①

方程①有实根，

则判别式Δ=4S2-16(S2-3)=48-12S2≥0，解得-2≤S≤2.

∴S=x+y的最大值为2.

解法二　椭圆+y2=1的参数方程为(θ为参数)，代入S=x+y,

得当θ=30°，即时，

S=x+y的最大值为2.

解法三　对椭圆和直线方程进行如下坐标变换：

令则则椭圆和直线方程分别变成

此时圆方程②和直线③仍有公共点，

则圆②的圆心O′(0，0)到直线的距离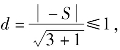

解得-2≤S≤2，故的最大值为2.