纵向思维：化繁为简的解题法

纵向化归是把面临的新问题，通过减元、降维等加工手段化归为已知(已解决)的问题，或是化归为熟悉的、简单的、具体的问题来处理，最后通过对新问题的解决而将原问题圆满解决，比如解不等式的化归过程是：

超越不等式→代数不等式→有理不等式→一次或二次不等式.

数列问题的化归过程是：

一般数列问题尤其是递推数列问题→等差或等比数列→结合等差或等比数列的性质求解.

解析几何问题的化归过程是:几何问题→函数或方程问题.

立体几何问题的化归过程是：空间问题(通过构造辅助平面)→平面问题.

例1　(1)当实数a取何值时，方程lg(x-1)+lg(3-x)=lg(1-ax)有一个实数解、两个实数解、没有实数解？

(2)定义区间(m，n)，[m，n]，(m，n]，[m，n)的长度为n-m，其中n>m.

由不等式组的解集构成的各区间长度的和等于6.

求实数t的取值范围.

解题策略　第(1)问是一道含参数对数方程的根个数的讨论，属于经典例题，可以运用代数的方法解，也可以运用数形结合的方法解，但不论是哪种方法，首先都要把超越方程化归为代数方程(x-1)(3-x)=1-ax(1<x<3)，然后再进一步求解.当然若采用数形结合法，关键在于构造函数，构造的函数不一样，解法也就各异，如方程(x-1)(3-x)=1-ax

可以变形为令探究这两个函数的交点个数问题；若直接令y=(x-1)(3-x)，y=1-ax(1<x<3)，可得数形结合的另一种解法，读者可以试一试，作个比较，看怎样的解法是最为简捷的.第(2)问，若设不等式的解集为A,不等式log2x+log2(tx+3t)<2的解集为B，则易得A=(-1,6)，而后一个不等式显然x>0，要得到不等式组解集的长度为6，易得x∈(0,6)，log2x+log2(tx+3t)<2应恒成立，则解题的思路明朗了，当然此时关键在于如何处理log2x+log2(tx+3t)<2这个超越不等式，应当化归为代数不等式组再进一步解下去！

解：(1)解法一　原方程可化为：(x-1)(3-x)=1-ax(1<x<3).

即x2-(a+4)x+4=0(1<x<3)，令f(x)=x2-(a+4)x+4.

由题意可知，

❶原方程有一个解等价于：f(1)f(3)≤0或

解上述不等式或不等式组可得：或a=0，经检验a=1不符合题意，

所以当或a=0时，原方程只有一个解.

❷原方程有两个解等价于：解此不等式组可得:

所以当时，原方程有两个解.

❸由❶❷可知，当a<0或a≥1时，原方程没有实数解.

解法二　原方程可化为：(x-1)(3-x)=1-ax(1<x<3)，即

令分别作出上述两个函数的图像.

根据图像交点的个数即可得与解法一同样的结论.

(2)不等式>1的解集A=(-1,6)，

设不等式log2x+log2(tx+3t)<2的解集为B，

∵不等式组的解集为A∩B，∴B⊆(0，+∞)，A∩B⊆(0,6).

∵不等式组的解集构成的各区间的和等于6，

∴不等式组在x∈(0,6)时恒成立，∴A∩B=(0,6).

等价于即

例2　(2018年高考江苏卷第12题)在平面直角坐标系xOy中，A为直线l：y=2x上在第一象限内的点，B(5，0)，以AB为直径的圆C与直线l交于另一个点D.若则点A的横坐标为________.

解题策略　本题把直线与圆，平面向量的数量积等知识汇合在一起，求相关点的坐标，当然可以从解析几何的角度求解，也可以平面向量为工具求解，解题时的切入点不同，解法也就不同.在同一系统内，可以从不同的角度思考，巧妙地转化，本题在几何中蕴含代数特征，如果引进某一个角，则可构造出三角函数用来处理解析几何问题，若借助平面几何相关知识(如垂径定理、圆周角定理、直径所对圆周角为直角等)，则可构造出用平面几何知识处理圆的相关问题，只要对题中蕴含的相关知识融会贯通，从中“悟”出的解题方法，往往都是优美的、赏心悦目的.

解法一　(构造法一：从直线与圆的交点切入)设A(a,2a)(a>0)，而B(5，0)，则圆心以AB为直径圆C的方程为(x-a)(x-5)+(y-2a)y=0,与直线l：y=2x联立，消去y并整理得：5(x-a)(x-1)=0.

可得x=1或x=a,则D(1,2).

当直线AB斜率不存在时，A(5，10)，C(5，5)，显然不符合要求，

由解得a=3或a=-1(不符合条件，舍去).

∴点A的横坐标为3.

解法二　(构造法二：从点到直线的距离切入)由于即AB⊥CD,而AC=DC，则∠DAC=45°.

∵圆C以AB为直径，∴∠ADB=90°,

点B(5,0)到直线l的距离为

设A(a,2a)(a>0)，则

解得a=3或a=-1(舍去).∴点A的横坐标为3.

解法三　(构造法三：以向量法切入)由题意可设A(a,2a)，D(b,2b)(a>0),则

∵圆C以AB为直径，则有又

解得

∴点A的横坐标为3.

解法四　(构造法四：引入三角知识结合斜率公式求解)由即AB⊥CD，而AC=DC，则∠DAB=45°.

设直线l：y=2x的倾斜角为α，则tanα=2,

则直线AB的斜率kAB=-tan∠ABO=-3.

设A(a,2a)，则由得a=3.∴点A的横坐标为3.

解法五　(构造法五：运用平面几何知识求解)由而AC=DC，则∠DAC=45°，而圆C以AB为直径，则∠ADB=90°，

设OD=m(m>0),由于直径l的斜率为2，可知

故DB=2m.(www.xing528.com)

在Rt△ODB中，m2+(2m)2=OB2=25,解得

在Rt△ADB中，可得由三角形的等面积法可得

解得yA=6,代入直线l:y=2x,可得xA=3,

图8-2

∴点A的横坐标为3.

例3　如图8-2所示，在斜三棱柱ABC-A1B1C1中，侧面ABB1A1与侧面ACC1A1成60°角，且两个侧面的面积之比为SABB1A1∶SACC1A1=8∶5，若这个棱柱的侧面积为60cm2，体积为且已知斜三棱柱的体积等于直截面面积与侧棱长之积，求侧棱长l.

解题策略　有关斜棱柱侧面积和体积的计算直接求解是困难的，可以通过斜棱柱的直截面这个辅助平面求解，斜棱柱的直截面就是与各条侧棱垂直且相交的截面，于是有S斜棱柱侧=直截面周长×侧棱；V斜棱柱=直截面面积×侧棱.因此，构造斜棱柱的直截面能方便快捷地求解斜棱柱的侧面积和体积(实质上已化归为平面问题).

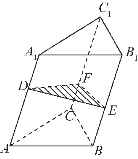
图8-3

解：作直截面DEF，如图8-3所示.则∠EDF=60°，

∵SABB1A1∶SACC1A1=(A1A·DE)∶(AA1·DF)=8∶5，∴DE∶DF=8∶5.

设DE=8x，DF=5x，由余弦定理得

由　得l=6(cm).

例4　(1)设F1，F2是椭圆的左右焦点，弦AB过点F2，求△ABF1的面积的最大值；

(2)过椭圆的左焦点F1作一直线交椭圆于P，Q两点，A为椭圆的右顶点，求△PAQ面积的最大值.

解题策略　本例两小题都是求与椭圆相关的三角形面积的最大值，由于两小题都涉及动直线问题，引进参变量显得很重要.第(1)问，设动直线AB的倾斜角为参数，则可扣住椭圆定义结合余弦定理获得一种巧妙的解法，其解题过程是把解析几何问题化归为三角函数问题，并通过换元化归为耐克函数性质的研究.第(2)问，以动直线PQ的斜率k为参数，则要分类讨论斜率不存在的情况，而且要求三角形面积的最值，由于解析式较为复杂，解题的技巧性很强，且方法也多，如可以通过变形化归为代数函数求最值，或通过去分母并换元化归为二次方程用判别式法求最值，还可通过三角换元与代数换元化归为“耐克函数”求最值.

解：(1)如图8-4所示，设∠xF2B=α(0<α<π)，|AF2|=m，|BF2|=n.

由椭圆的定义知

图8-4

在△AF2F1和△BF2F1中，应用余弦定理，得

∴S△F1AB

令

在(0，1]上是增函数，

∴当t=1即时，故△ABF1的面积的最大值为

(2)F1(-1，0)，A(2，0)，且当直线PQ的斜率不存在时，|y1-y2|=3.

当直线PQ的斜率存在时，设直线PQ的方程为y=k(x+1)(k≠0)，P(x1y1)，Q(x2y2)，

联立方程组消去x并整理得(3+4k2)y2-6ky-9k2=0.

显然Δ>0，

∵|y1-y2|

∴设

下面用多种方法求f(k)的最大值.

解法一　设k=tanθ，其中

则设t=|sinθ|,t∈(0,1).

则在t∈(0,1)上是减函数，

当时，综上，△PAQ面积的最大值为

解法二　m(k)

令则

又∵函数g(t)在上是减函数，即当

综上，△PAQ面积的最大值为

解法三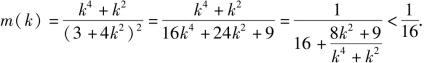　

当时，由解法一得

综上，△PAQ面积的最大值为