化归与辩证思维方法的优化

匈牙利数学家路沙·彼得指出：“数学家往往不是对问题实行正面的攻击，而是不断地将它变形，直至把它变成能够得到解决的问题”，讲的就是数学解题中化归的思维方法，其在作品《无穷的玩艺——数学的探索与旅行》一书中对“化归”作过生动而风趣的描述：“假设在你面前有煤气灶、水龙头、水壶，你想烧开水，该怎样去做？”正确的回答是：“在水壶中放上水，点燃煤气，再把水壶放到煤气灶上.”接着路沙又提出第二个问题：“如果其他的条件都没有变化，只是水壶中已有足够多的水，那么你又应当怎样去做？”对此，人们往往回答说：“点燃煤气，再把壶放到煤气灶上.”但路沙认为这并不是最好的回答，因为“只有物理学家才这样做，而数学家则会倒去壶中的水，并且声称他已经把后一问题化归成先前的已经得到解决的问题了.”

路沙·彼得的比喻固然有点夸张，但这种思维方式对数学家来说是十分典型的，道出了化归的根本特征.这就是说，在解决问题的过程中，数学家往往不是直接解决原问题，而是把所要解决的问题经过某种变化，使之归结为另一个问题，再通过另一个问题的求解，把解得的结果作用于原问题，从而使原问题得解，这种解决问题的思想，我们称之为化归思想.

所谓“化归”，从字面上看，可以理解为转化和归结的意思.在对问题作细致观察的基础上，展开丰富的联想，以求唤起对有关旧知识的回忆，开启思维的大门，顺利地借助旧知识、旧经验来处理面临的新问题，化归思想的实质是通过事物内部的联系和矛盾运动，把所需要解决的问题转化为已经解决的问题，或容易解决的问题，同原问题相比，化归后的新问题必须是已经解决或较为熟悉、简单的问题，它是数学中最重要、最基本的思想之一.

利用化归解决问题的过程如图8-1所示.

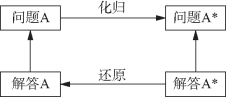
图8-1　利用化归解决问题

解题是数学学习的一个最基本的形式，运用辩证的思想和方法探索问题、分析和研究问题、解决问题，是培养学生辩证思维，提高数学解题能力的有效途径.将一个非基本的问题通过分解、变形、代换或平移、旋转、伸缩等多种方式，将它化归为一个熟悉的基本问题，从而求出解答，这一过程其实也是辩证思维的过程.

数学中充满着矛盾、运动和变化，充分体现了辩证思想，包括如下几个重要方面：对立统一思想、互变思想、转换思想、一分为二思想等，具体表现在下列方面.

(1)“熟悉”与“陌生”：数学解题过程也就是把陌生的问题通过适当变换、逐步转化为熟悉的问题，化陌生为熟悉起到推陈出新、化难为易的作用.

(2)“合”与“分”：从辩证思维的角度分析数学解题中的分与合，就是化整为零和聚零为整思想的应用，即在解题过程中先将原问题进行分解、化归为较易解决的小问题，各个击破再合成，从而得原问题在整体下的解，这是以分求合的思想，反之也可以合求分.(www.xing528.com)

(3)“正”与“逆”：一般解题过程总是先从正面入手，进行思考，但有时会遇到从正面入手不易解决，这时应该从问题的反面去思考，这就是“正难则反”，这样解题会收到意料不到的功效，这种“逆”恰好弥补了“正”的不足.

(4)“动”与“静”：有些数学问题往往是“静”在其表，而动在其“里”，动和静是事物状态表现的两个侧面，可用动态的观点来处理静的形态和数量关系,即以动求静,当然也有用静态的观点来处理运动过程及其对象，即以静求动.因此，在求解数学题时，要善于利用“变动”的思想，动中求静，静中思动，培养思维的灵活性.

(5)“进”与“退”：在数学问题的求解过程中既要能“进”，更要能“退”，采用以退求进，进退结合的方法寻求解题途径.如分析法是由结论向条件退，把空间问题转化为平面问题则是由高维向低维退，由抽象的数学问题向具体的几何模型退.“退”为了“进”，进而解决原问题，这是一种经常用到的辩证思维.

(6)“一般”与“特殊”：“一般”概括了“特殊”，“一般”比“特殊”更能反映事物的本质，命题的一般结论可以从特殊情况中反映出来，而特殊情况往往是更具体化、简单化，从而易于入手，发现解题规律，数学中的归纳思想，也可以看作是从特殊到一般的转换的思想.

(7)“强化”与“弱化”：很多较难的数学题，一般可采用“弱化”的方法进行思考，但也有些题目，采用“强化”的方法考虑更能奏效.

(8)“抽象”与“具体”：抽象是在对事物进行的由表及里、去粗取精、去伪存真的基础上，抽取提炼出事物的本质属性，舍弃事物的非本质属性，借以形成科学的概念和揭示事物的发展规律的一种思维.具体就是把抽象的概念、结论和规律表现于直观、简单、清晰明确的对象或问题.而人们认识发展的具体过程常表现为：感性具体—抽象—综合—理性具体.这就是我们运用具体与抽象的转换思想解题的路线图.

(9)“直”与“曲”：直与曲是两种不同的形象，从其几何特征看，前者曲率是零，后者曲率不是零；从解析表达式看，前者为直线方程，后者是非直线方程，直与曲的对立是极为明显的，但也能够统一.实际上，曲直转换的思想早在我国古代就产生了，数学家刘徽在为前人著作《九章算术》加注时，就在论述割圆术时明确指出了曲直转换的方向：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣.”当然，曲与直互相转换的思想方法是在微积分中才真正地实现的.立体几何中有关曲面上的问题，直接求解比较困难，往往把它展开成平面图形，使曲面(或折面)有关问题转化为平面上的问题，使曲线(或折线段)能化为直线段的问题去求解,运用“曲”向“直”的转化能化难为易.

(10)“主”与“次”：一般而言，代数中的含参数问题以及解析几何中的含参数问题都有一定难度，对这类问题的解决，有时需对参数的意义，特别是对主元与次元进行转换，也就是“变元”，起到化难为易、化繁为简的作用，具体为：①变换主元、次元的位置；②引入参数代替题中的主元；③消去主元，使次元升为主元，这些都体现了辩证思想的运用.

用辩证思想解题，除了上述十大关系的转换之外，还有整体与局部的转换、有限与无限的转换、或然与必然的转换、正运算和逆运算的转换、高级运算与低级运算的转换等.另外，互变思想也是辩证思想的重要组成部分，包括常量与变量的互变，因果关系的互变、质与量的互变等.

化归与辩证的思想使我们感悟到：一切固定差别都消失了，一切都可以用相对或相反的形式表示出来,而这种从一种形态到另一种相对或相反形态的转换，并不是无聊的游戏，它是数学科学的最有力的杠杆之一.