命题之间的转化与变换的优化措施

用命题转化策略解数学问题的过程如图7-17所示.

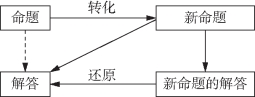
图7-17　命题转化策略

就是说在解决问题时，将原问题进行变形，使之转化，直至最终归结为我们熟悉的，或易于解决的，或已经解决的问题，命题之间的转化与变换的基本方向就是“把未解过的题目归结为已经解过的题”，使复杂问题简单化、难解问题容易化、未知问题已知化、抽象问题具体化.

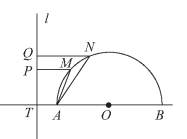
图7-18

例1　如图7-18所示，已知半圆O的直径为AB，l为位于半圆之外，而又垂直于BA延长线的一直线，其垂足为T，且又M，N是半圆上的不同的两点，NQ⊥l，MP⊥l，且求证：|AM|+|AN|=|AB|.

解题策略　如果限于平面几何的方法证明本例，则较困难，但若使用RMI原理，即关系(Relation)、映射(Mapping)、反演(Inversion)原理将此几何问题映射为代数问题，运用代数变换方法先寻求代数结论，再反演为几何结论，则就方便多了.本例条件中给出了以AB为直径的半圆，又给出了即动点到定直线的距离等于到一定点的距离，显然符合抛物线的定义，如果以A为极点，AB所在射线为极轴建立极坐标系，则本题可以用下述过程来求解，如图7-19所示.

图7-19　解题过程

推广到一般，RMI原理解题的过程(即命题之间的转化与变换)如图7-20所示.

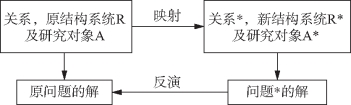
图7-20　RMI原理解题过程

证法一　以A为极点，射线AB为极轴建立极坐标系，设

则半圆方程为

设M(ρ1，θ1)，N(ρ2，θ2)，则|AM|=ρ1，|AN|=ρ2，且

又由题图知|MP|=ρ1cosθ1+a，|NQ|=ρ2cosθ2+a，

而即|MP|=|MA|，

∴ρ1cosθ1+a=ρ1　　③

同理ρ2cosθ2+a=ρ2　　④

由①③得　　⑤

由②④得　　⑥

式⑤⑥说明ρ1，ρ2是方程ρ2-2Rρ+2Ra=0的两根.

∴按韦达定理有ρ1+ρ2=2R,故|AM|+|AN|=|AB|.

证法二　以A为极点，射线AB为极轴建立极坐标系.根据已知条件及抛物线定义，可知M，N两点是以A为焦点，l为准线的抛物线上的两点，而抛物线方程为以此与半圆方程联立，同样可证得ρ1+ρ2=2R.

例2　已知数列{an}各项为正数，且满足求数列{an}的通项公式.

解题策略　非等差数列、非等比数列的问题常通过构造辅助数列转化为等差数列或等比数列求解，构造法使转化与化归的数学思想显得更加丰富多彩.

解：将等价变形为

同理可得2-an>0，令bn=2-an，则

两边取对数得lgbn+1=2lgbn-lg2.

变形为lgbn+1-lg2=2(lgbn-lg2)，且lgb1-lg2=-lg2≠0.

∴数列{lgbn-lg2}是以-lg2为首项，2为公比的等比数列.

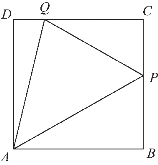
图7-21

∴lgbn=(-lg2)·2n-1+lg2=(lg2)(1-2n-1)=lg21-2n-1，(www.xing528.com)

∴bn=21-2n-1，即2-an=21-2n-1.∴an=2-21-2n-1.

例3　如图7-21所示，已知正方形ABCD的边长为1.点P，Q分别在BC，CD上，△CPQ的周长为2.

(1)求PQ的最小值；

(2)试探究∠PAQ是否为定值?若是定值，请给出证明；若不是定值，请说出理由.

解题策略　第(1)问，可通过引入∠CPQ=θ为参数，将PQ转化为含θ的函数，求三角函数的最值；第(2)问，可通过引入参数α，β，将探究∠PAQ的定值问题转化为探究tan(α+β)为定值的问题，并由此强化构造直角三角形解题的意识，当然探求的过程可以不相同，但只要思维是合理的，便可在理性分析的基础上选择运用.如本小题，设DQ=x，BP=y，由条件易得x+y=1-xy，可以借助余弦定理或通过建立直角坐标系运用的数量积公式求角，但运算量均较大，这样的思考对于本题而言，合理性不够.一般而言，“坐标法”是应坚持的解题的重要方法，但应克服“习惯性”偏爱“坐标法”解题的习惯，寻找更为巧妙的解题途径.

解：(1)设∠CPQ=θ，则依题意，△CPQ的周长为2=CP+PQ+CQ=PQ(1+sinθ+cosθ)，于是

当时，PQ取最小值此时

(2)解法一　设DQ=x，BP=y，依题意，

即亦即1-x-y=xy，

设∠DAQ=α，∠BAP=β，则

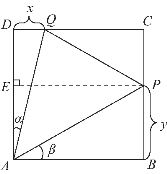
图7-22

又且

故(定值).

解法二　同解法一得x+y=1-xy，

易得

或者作PE⊥AD，垂足为E(如图7-22所示)，则

由此可得

由得即(定值).

例4　已知定点A(-1，0)和B(1，0)，P是圆(x-3)2+(y-4)2=4上的一动点，求的最大值和最小值.

解题策略　这是一道解析几何问题，若设P(x，y)，由距离公式写出为x，y的二元函数，消元很不方便，若设P(3+2cosθ，4+2sinθ)，由距离公式写出的三角函数式，则原问题转化为三角函数求最值.但解题过程仍然较烦琐，因为O是AB的中点，所以若利用向量转化为求向量的最值问题，则解题过程相对简捷.

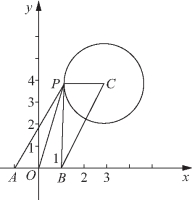
图7-23

解：如图7-23所示，设已知圆的圆心为C，由已知可得

又由中点公式得

又点P在圆(x-3)2+(y-4)2=4上，且

即

故的最大值为100，最小值为20.