高次向低次的转化与变换讲解

对于含参数的高次方程，而参数的次数比较低，可运用“主元法”，视参数为主元，解参数为主元的方程，从而达到降次的目的，再解之，则简单许多，对于高次的分式函数，可根据其结构特征采用三角换元法向低次转化才能求解，有些数学题，直接解答难以入手或十分烦琐，特别是复杂的分式问题，利用倒置变换的方法求解，可化难为易.

例1　若关于x的方程有4个不同的实数解，则k的取值范围为(　　).

解题策略　本题实质是高次方程又是分式方程，求解的方向必是降次，若能注意到对任意的k∈R，x=0必是原方程的一个根，则降次就很容易了，问题顿时得到了简化.

解：=kx2有4个实数解，显然，x=0是方程的一个解，下面只考虑x≠0情形，且有3个实数解即可.

若x>0，原方程等价于1=kx(x+4)，显然k≠0，则

要使该方程有解，必须k>0，则此时x>0，方程有且必有一解；

图7-15

则当x<0时必须有两解，当x<0时，原方程等价于-1=kx(x+4)，即画出函数图像如图7-15所示(注意x<0且x≠-4)，要使该方程有两解，必须解得这也是上述几种情况的公共部分，故为所求，选C.

例2　(1)解关于实数x的方程x4-6x3-2(a-3)x2+2(3a+4)x+2a+a2=0，其中a∈R；

(2)x3+ax2+bx+c=0的3个根分别为a，b，c，并且a，b，c是不全为零的有理数，求a，b，c的值.

解题策略　第(1)问，直接解关于x的4次方程是相当困难的，但转换x与a的位置形式，把原方程看作关于a的二次方程，则直接可用十字相乘法再转换为两个关于x的二次方程，用求根公式解，因为x是实根，故判别式不能忘.第(2)问，找出a，b，c三者的关系可以借鉴二次函数的零点法，当然也可以直接利用一元三次方程的韦达定理来处理，此外，如果高次方程有有理根，那么该有理根应是常数的约数.

解：(1)原方程可变为关于a的二次方程a2-2(x2-3x-1)a+x4-6x3+6x2+8x=0，方程左边利用十字相乘法分解得(a-x2+2x+2)(a-x2+4x)=0，从而转化为两个关于x的二次方程x2-2x-2-a=0，x2-4x-a=0.

解上述两个方程得，当a>-3时，原方程有4个实根，

当-4≤a≤-3时，原方程有两个实根，

当a<-4时，原方程无实根.

(2)由题意可设x3+ax2+bx+c=(x-a)(x-b)(x-c)，

则x3+ax2+bx+c=x3-(a+b+c)x2+(ab+ac+bc)x-abc，(www.xing528.com)

从而有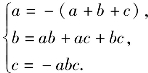由c=-abc得c=0或ab+1=0.

若c=0，则有当b=0时，a=0，与条件不符，故b≠0，∴a=1，从而b=-2.

若ab+1=0，则有消去c得2a2+b2+b-2=0.

即b4+b3-2b2+2=0，也就是(b+1)(b3-2b+2)=0.

由于b是有理数，而方程b3-2b+2=0无有理根，故b=-1，从而a=1，c=-1.

综上：a=1，b=-2，c=0或a=1，b=-1，c=-1.

例3　设k≥9，解关于x的方程x3+2kx2+k2x+9k+27=0.

解题策略　由于原方程是关于x的三次方程，难于直接求解，但是注意到参数k的最高次幂是2，而且题中给定了k的范围，进行参数与未知数的角色转变，将原方程看成是关于k的二次方程(即高次向低次转化)，就可得到x与k之间的数学关系，再利用给定的k的范围来求出x即原方程的解.

解：x3+2kx2+k2x+9k+27=xk2+(2x2+9)k+x3+27=0.

将其看成关于k的二次方程，则Δ1=(2x2+9)2-4x(x3+27)=9(2x-3)2,

∴k=-x-3或或x2+(k-3)x+9=0.

对于方程x2+(k-3)x+9=0，其Δ2=(k-3)2-4×9=(k-9)(k+3).

∵k≥9,∴Δ2≥0.

例4　函数 的最大值与最小值的乘积等于________.

解题策略　由于所给函数是高次的分式函数，形式又较复杂，只有向低次转化才能求解，而三角换元法及三角降次公式有此功效，由于x∈R，可令x=tanθ，则解之不难.

解：令x=tanθ，代入并化简得

即故