高维向低维的转化与变换探讨

事物的空间形成，总是表现为不同维数且遵循由低维到高维的发展规律.把维数、抽象水平较低的或局部的问题转化为维数、抽象水平较高或整体性较强的整体间的关系问题，通过对整体性质或关系的考虑，而使原问题获得解决的策略即升维策略，如平面图形通过翻折或旋转成为空间图形就是二维向三维的转化与变换，这种方法也叫升维法.也可考虑把高维空间的问题转化为低维空间的问题，这种处理问题的方法叫降维法，或称之为降维策略，如将立体几何问题转化为平面几何问题.这种把问题由一个领域转换到另一领域寻求解决之道的解题策略，在复数、行列式与立体几何中应用广泛.

例1　曲线C1是以原点O为中心，F1、F2为焦点的椭圆的一部分；曲线C2是以O为顶点，F2为焦点的抛物线的一部分，设A是曲线C1和C2的交点且∠AF2F1为钝角，若

(1)求曲线C1和C2的方程；

(2)过F2作一条与x轴不垂直的直线，分别与曲线C1，C2依次相交于B，C，D，E这4点，若G为CD中点，H为BE中点，则是否为定值？若是，求出定值；若不是，说明理由.

解题策略　本题中涉及平面上众多的两点间的距离，且有多个字母或未知数，会给解题带来困难，的结构也颇复杂，得到的二元代数式很难化简，无法操作.若运用投影后把二元化为一元，则使问题变得简单，而题中直线过x轴上一定点，相关点向y轴作投影亦可减少运算量，求之不难.

解：(1)设椭圆方程为则2a=|AF1|+|AF2|=6，得a=3.

图7-8

如图7-8所示，设A(x，y)，F1(-c，0)，F2(c，0)，

则

两式相减得由抛物线的定义可知

解得或(舍去)，

∴椭圆C1的方程为抛物线C2的方程为y2=4x.

(2)设B(x1，y1)，E(x2，y2)，C(x3，y3)，D(x4，y4).

把直线x=ty+1代入得(9+8t2)y2+16ty-64=0，则

同理将x=ty+1代入y2=4x，得y2-4ty-4=0，则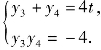

则

故是定值，定值为3.

例2　在△ABC中，且动点P使得成等差数列，当A最大时，求的取值范围.

解题策略　本题初看是平面向量问题，又涉及三角与数列知识，同解三角形似乎也有关系，信息量大，解题的难度较高，若能通过“降维策略”，即通过一条内在的线索把种种条件串起来朝单一的方向靠拢，问题顿时变得简单，由条件成等差数列，则则P是椭圆上一动点，B，C是椭圆的焦点，△ABC与此椭圆也有关联，结合题设条件确定最大角A，也就确定了点A的坐标，从而将问题转化为一个定点A与椭圆上一个动点P的距离的取值范围的求解.可见，我们讲的降维策略不局限于将三维问题(空间)降为二维(平面)问题，将二维问题(平面)降为一维(直线)问题，“降维策略”也可以引申为将复杂的、陌生的、困难的、众多知识交叉的难度维数高的问题转化为简单的、熟悉的、单一的问题.

解：以BC所在直线为x轴，以边BC中垂线为y轴，建立平面直角坐标系(如图7-9所示).

图7-9

由于

依据椭圆定义可得动点P的轨迹方程为故设

由

又(www.xing528.com)

此时即△ABC为等腰三角形.

故A(0，1)，依据两点间距离公式可得

故

例3　(1)如图7-10所示，在直三棱柱ABC-A1B1C1中，底面为直角三角形，是BC1上一动点，则CP+PA1的最小值是________；

(2)如图7-11所示，圆台的上底面半径为2cm，下底面半径为4cm，母线长为6cm，求轴截面相对顶点A，C在圆台侧面上的最短距离.

图7-10

图7-11

图7-12

解题策略　不论是多面体还是旋转体，从表面走或从不同的平面走的最短距离总是设法把空间图形转化为平面图形(由三维向二维转化)，多面体是把不同的面“打开”成同一平面，旋转体通常把侧面展开，第(1)问，联结A1B，沿BC1将△C1BC展开与△A1BC1在同一平面内；第(2)问，空间图形→平面图形，即展开圆台侧面，A，C两点所成的线段长即为所求的最短距离.

解：(1)如图7-12所示，联结A1，B，沿BC1将△C1BC展开与△A1BC1在同一平面内，联结A1，C，则A1C的长度就是所求的最小值，通过计算可得∠A1C1C=90°，又∠BC1C=45°.∴∠A1C1C=135°，由余弦定理可求得

图7-13

(2)如图7-13所示为沿母线AD剪开后将圆台侧面展开所得展开图，问题转化为求展开图中线段AC的长.

设圆台的上底面、下底面半径分别为r1，r2，因为侧面展开图圆心角

且B，C分别为所在弧的中点，所以在等腰三角形AOB中，得△AOB是等边三角形，因为所以OC=6，而BC=6，C为OB的中点，所以即A，C两点在圆台侧面上的最短距离为

例4　空间有4个球，它们的半径分别为2，2，3，3，每个球都与其他3个球外切，另外有1个小球与这4个球外切，求小球的半径.

解题策略　把立体问题化归为平面问题是解决立体几何问题的基本策略，本例是一个颇为复杂的立体问题，这里涉及多组三球两两相切，三球圆心及切点在同一平面内，所以完全可以化归为平面问题，把三维转换成二维来解决，这就是著名数学家波利亚说的“不断地变换你的问题”的策略：“我们必须一再地变换它，重新叙述它，直到最后成功地找到某些有用的东西为止.”

解：如图7-14(a)所示，O1和O2是半径为2的两个小球的球心，O3和O4是半径为3的两个小球的球心，O是未知半径小球的球心，E和F分别是两个半径为2的小球的切点和两个半径为3的小球的切点，根据对称性，可以断定O是在EF上，EF=EO+OF.

(a)

(b)

图7-14

在图7-14(a)中，O1O2=4，O3O4=6，其余由两个圆心构成的线段长度都为5，很容易通过计算求得在图7-14(b)中，设圆O的半径为R，那么同理所以解方程得或-6，因为球的半径不可能是负值，所以小球的半径只能是