在寻找解题思路遇到困难的时候，不妨通过挖掘已知条件的内涵，发现式子的几何意义，利用几何图形的直观性解决问题，若在解题过程中遇到令人望而生畏的繁杂运算，不妨借助图形去开辟新路；在需要检验结论的正确性时，也不妨借助图形去验证，这是以形助数的解题策略，当然构造图形是个技术活，需要积累，更需要联想，但是光有以形助数是不够的，正如华罗庚先生所言：“数无形时少直观，形少数时难入微.”我们还要善于用数解形，借助数量的计算和分析，使问题的解决严谨化、精确化.
例1 设
求证：sinx<x<tanx.
解题策略 本例用代数法直接证明比较困难，如果能将要证明的不等式构造成相应的图形，利用图形中的面积关系(局部小于整体)论证，显得直观清晰.
证明 如图7-4所示，作一个半径为1，圆心角为x的扇形
且BC⊥OD，AD⊥OD，易得△OBD的面积为
图7-4
扇形
的面积为
△OAD的面积
结合图形，根据局部必小于整体，明显有：
S△OBD<S扇形
<S△OAD.
∴sinx<x<tanx.
例2 已知A(1，1)为椭圆
内一点，F1为椭圆的左焦点，P为椭圆上一动点，求|PF1|+|PA|的最大值和最小值.
解题策略 求解有关圆锥曲线的最值问题，通常建立函数表达式，利用函数与方程的思想解决，但有时这种解法不一定行得通，有时函数表达式很难建立，即使辛辛苦苦建立起来，求最值也难以操作，这时，若能结合图形，考虑用圆锥曲线的定义来解，有效且显得特别简单.
解：由
可知
左焦点F1(-2，0)，右焦点F2(2，0)，由椭圆定义，知|PF1|=2a-|PF2|=6-|PF2|，
∴|PF1|+|PA|=6-|PF2|+|PA|=6+|PA|-|PF2|，
图7-5
如图7-5所示，由
知
当点P在AF2的延长线上的点P2处时，取右“=”；
当点P在AF2的反向延长线上的点P1处时，取左“=”，
即|PA|-|PF2|的最大值、最小值分别为
于是|PF1|+|PA|的最大值是
最小值是
例3 如图7-6所示，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA，PB，切点分别为A，B，求证：∠AFP=∠BFP.
解题策略 本例是直线与抛物线的位置关系问题，证明当动点P在已知直线上运动，过点P作抛物线的切线PA，PB，A，B为切点，F为抛物线焦点，证明无论P在已知直线上怎样运动，始终有∠AFP=∠BFP，而角度问题与向量的数量积关系紧密，所以可从数量积入手，把几何关系转化为数量关系，通过“计算”(这里是数量积的坐标运算)可得出所证的结论.(www.xing528.com)
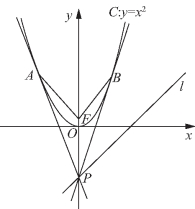
图7-6
证明 设切点A，B的坐标分别为
和
可得切线AP的方程为
切线BP的方程为
解得点P的坐标为
则
由于点P在抛物线外，即
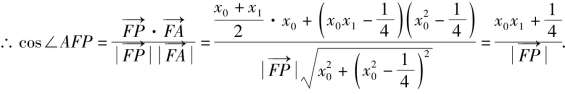
同理有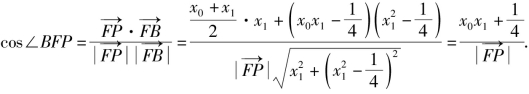
综上可知∠AFP=∠BFP.
例4 a，b，c均大于零，且a2+b2+c2=1.求证：
解题策略 根据条件a2+b2+c2=1，可将待证式变更为
观察左端各根式形状结构联想到勾股定理，似可构造长方体来解决问题，一道较为复杂的条件不等式证明题立即有了明朗的证明方向，真可谓“柳暗花明又一村”.
证明 构造以a，b，c为三条棱的长方体ABCD-A1B1C1D1，如图7-7所示，其中AA1=a，A1B1=b，A1D1=c.
图7-7
由a2+b2+c2=1，知长方体的体对角线长为1，联结AB1，AD1，AC1和A1C1，
有
在△AB1C1中，∵AB1+B1C1>AC1,
同理，
三式相加并整理，即得
亦即
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
