多元与一元之间的转换与变化

在一个数学问题中有多个字母或未知数会给解题带来困难，解决问题的方法是想办法消去过多的字母，从而使问题变得简单，消元思想就是由一些元素间的已知等量关系，通过有限次的变换消去其中某些元素，从而得出其他一些元素之间的等量关系的解题思想，通常用代入、加减、乘除、代换等方法消元，三角换元法在多元向一元的转化与变换中显示出其特有的功能.

例1　已知a>0，a≠1，试求使方程loga(x-ak)=loga2(x2-a2)有解的k的取值范围.

解题策略　本例所给的方程内含有x，a，k三个变元，任意选取一个当作主元，均可解出正确结果，当然解题过程并不简单，如果利用三角代换，可轻松实现从多元向一元的变换，则可简化解题过程.

解：原方程等价于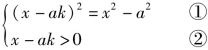

可令

代入①，整理得，

再由方程(x-ak)2=x2-a2解出代入②得到不等式

∴k∈(-∞，-1)∪(0，1).

例2　已知x2-xy+y2=1，求x2-y2的取值范围.

解题策略　本例条件等式x2-xy+y2=1含有二个变元x,y且有xy项，直接代入消元，很难实现，若采用三角换元化为一元(一个角)则解之不困难了，实现这一目标关键是对x2-xy+y2=1变形，与三角公式挂起钩来.

解：故可设

则

x2-y2

例3　设x，y∈R且3x2+2y2=6x，求x2+y2的取值范围.

解题策略　本例可用上例类似的解法，即三角换元法，也可以转化为二次函数求值域，不管是哪一种方法，多元变一元的解题途径是一致的.

解：解法一　由3x2+2y2=6x得3(x-1)2+2y2=3，即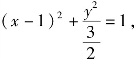

设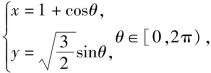

则x2+y2

∵cosθ∈[-1，1]，∴当cosθ=1时，(x2+y2)max=4；当cosθ=-1时，(x2+y2)min=0.(www.xing528.com)

∴x2+y2的取值范围是[0，4].

解法二　由6x-3x2=2y2≥0得0≤x≤2，设k=x2+y2，则y2=k-x2，代入已知等式得x2-6x+2k=0，即其对称轴为x=3.

由0≤x≤2，结合函数的单调性得k∈[0，4]，

∴x2+y2的取值范围是[0，4].

例4　(1)已知实数x，y满足方程(x+2)2+y2=1，求的最小值；

(2)若实数x，y满足方程x2+y2-2x-4y+1=0，求代数式的取值范围.

解题策略　本例两小题都是圆上动点与圆外一定点连线的斜率问题，通过数形结合求解很方便，这里考虑换一个角度思考，即如何把二元问题转化为一元问题？通过构造向量的方法能实现这一目标，别具一格.

解：(1)设=k，则y-1=kx-2k，y=kx-2k+1.

设则

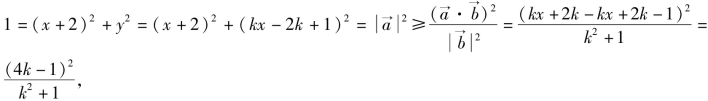故(4k-1)2≤k2+1，得k(15k-8)≤0，解得

则的最小值是0.

(2)设=k，则y=kx+2k　　①

∵方程x2+y2-2x-4y+1=0可化为(x-1)2+(y-2)2=4

故可将①式写成3k-2=-k·(x-1)+1·(y-2).

构造向量

则

由得(3k-2)2≤4(k2+1)，解得

故所求的取值范围是