有限与无限之间的转化与变换：第三十九讲优化建议

有限与无限的思想方法，也是一种思维方法，一种解决数学问题的方法，考试中心对考试大纲的解读中指出：“高考中对有限与无限的思想的考查才刚刚起步，并且往往是在考查其他数学思想和方法的过程中同时考查有限与无限的思想.比如，在使用由特殊到一般的归纳思想时，含有有限与无限的思想；在使用数学归纳法证明时，解决的是无限的问题，体现的是有限与无限的思想，等等.”

中学数学中占有重要地位的极限思想，从中学数学教学角度看，着重从直观上考查无穷运动，从有限中认识无限，从近似中认识精确，从量变中认识质变，形象地展现了有限与无限之间的转化与变换.

例1　在正n棱锥中，相邻两侧面所成的二面角的取值范围是(　　).

解题策略　本题考查的是一个有限图形，即正n棱锥的侧面所成的二面角的问题，但是解决这个问题并不容易，我们可以将有限的问题用无限的方法来求解.

解：设正n棱锥的顶点为P，底面为α，高为h，相邻两侧面所成的二面角为θ.

考虑顶点P的两个无限趋近的情形：

❶当顶点P无限趋近于底面α时，正n棱锥无限趋近为底面正n边形，这时，相邻两侧面所成的二面角无限趋近于平面，即θ→π；

❷当顶点P向上趋近于无限高时，正n棱锥就无限趋近于正n棱柱，这时，相邻两侧面所成的二面角为正n边形的内角，即

由以上，应排除A，C，D，故选B.

例2　对任何x∈(1，a)，都有(　　)成立.

A.loga(logax)<logax2<(logax)2　　　B.loga(logax)<(logax)2<logax2

C.(logax)2<logax2<loga(logax)　　　D.logax2<loga(logax)<(logax)2

解题策略　本题的解答用极限法处理别开生面，易得结论.因为x∈(1，a)，x值的极端情形是x→a，可以发展以a为底数的对数的极端情形.

解：当x→a时，logax→1，(logax)2→1，logax2=2logax→2，loga(logax)→0，

故否定了A、C、D的正确性，选B.

例3　已知抛物线方程y2=2px(p>0)，试问：在x轴正方向上是否必存在一点M，使得对于抛物线上任意一条过M的弦PQ均有为定值.

解题策略　若符合条件的点M存在且点M在x轴正方向上，过点M的弦有一个特殊位置，这条弦垂直于x轴时，可以首先以此进行探讨；而且点M还有两个极限位置，即点M趋近于原点或趋近于无穷远点，以此探究弦PQ的状况.由此可见，对于解答某些数学问题，可以从无限或极端状态的角度去思考，从而得到数学关系的猜想，这种猜想往往正是所要寻求的结论.当然，猜想仍需要在一般情况下加以证明.

解：假设符合条件的点M存在，考虑过点M的一条特殊的弦——垂直于x轴的弦的情形.设M(x0，0)，P0(x0，y0)，Q0(x0，-y0)，则

但是仅凭此式还看不出点M的位置，

再考虑过点M的弦的极限情形——x轴的正半轴，此时过点M的弦PQ的一个端点是原点，另一个端点可看成是无穷远点，有MP→+∞，则

于是于是可猜得定点M(p，0).

下面证明过点M(p，0)的任意一条弦PQ均有为定值.

设过点M的直线方程为代入抛物线方程，得

t2sin2α-2ptcosα-2p2=0.

设方程的两个根为t1，t2，它们的绝对值的几何意义分别为MP及MQ的长，(www.xing528.com)

则

故存在符合条件的点M，且点M为(p，0).

例4　设数列{an}的前n项的和

(1)求首项a1与通项an；

(2)设证明

解题策略　本例的难点在第(2)问，从常规思路看，为了求和，需要对Tn变形，才能求但不一定能想到变形的方法，一旦想不到，后面的运算就无法进行，为此，我们试着换一种思路，先用特殊的数值作一些尝试得到一个猜想，再用数学归纳法证明这个猜想，使问题从有限向无限转换.

解：(1)容易得出a1=2，an=4n-2n(n∈N*).

(2)证法一　先求出Tn，再对Ti裂项，从而进一步求和.

把an=4n-2n代入题设的Sn的表达式中，得

Tn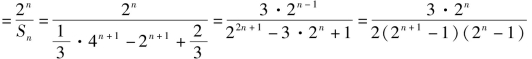

上述解法中对Tn用了裂项方法，为求创造了条件，但这个方法虽然巧妙，却不容易想到，于是有了下面的解法.

证法二　证明对所有正整数n，不等式成立.这是一个与正整数n有关的问题，可以考虑用数学归纳法，但是不等式的右边是一个常数从n=k延续到n=k+1的证明就比较困难，因此用特殊的数值作一些尝试.

若n=1，则

若n=2，则的变形是类比n=1得到的)；

若n=3，则的变形是类比n=1和n=2得到的).

由以上，可以猜想为求证(把结论加强).

下面用数学归纳法证明：

❶当n=1时，不等式成立；

当n=2时，

∴n=1，2时，不等式成立.

❷假设当n=k(k≥3)时，不等式成立，即

那么，当n=k+1时，有

即当n=k+1时，不等式成立.

于是，对n∈N*不等式成立，即