正与反的转化与变换的优化

对于某些数学问题，当从正面思考难以解决时就转向反面思考，当用直接解法不能奏效时就转用间接解法，当命题难以被证明时就转而举反例加以否定，特别是否定性命题，常要利用正反的相互转化.一般地，题目若出现多种成立的情形，则不成立的情形相对较少，从反面考虑较简单.有些命题直接证明难度较大，正难则反，可以采用反证法.

例1　(1)求证：方程sinx+c=x有唯一解；

(2)若方程cos2θ+6sinθ+a-2=0在时有解，求实数a的取值范围.

解题策略　第(1)问是唯一性命题的证明,直接证明有些困难，可从反面考虑，命题的反面是此方程至少有两解，反证法是从反面的角度思考问题的证明方法，属于“间接证明”的一类.第(2)问，将原方程变形为2sin2θ-6sinθ-a+1=0.直接讨论当时有解求参数a的取值范围，不易解决.若设t=sinθ,则得关于t的二次方程再进行讨论可求a的取值范围，但显得烦琐.若两个变元sinθ和a转换一下角式，用sinθ表示a，可轻松求解，此谓正难则反，逆向考虑，反客为主.

解：(1)证明　设至少有两解x1，x2，则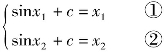

①-②，得sinx1-sinx2=x1-x2

 ③

另一方面，由x1≠x2,知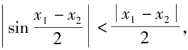这与③式矛盾，假设不成立，原命题成立，∴sinx+c=x只有唯一解.

(2)

当时有于是即

故方程有解时，实数a的取值范围为

例2　(2010年北京大学自招试题)是否存在使得sinx,cosx,tanx,cotx为等差数列？

解题策略　本题的本质是一道三角函数方程解的存在性问题，我们可以在假设问题的结论有解的前提下，来探求满足题设条件的根是否存在,由于sinx,cosx,tanx,cotx为等差数列的充要条件是：而这组三角方程在内是否有解？若有解，则假设成立，若无解，则说明问题的结论是否定的.

解：若存在这样的x，使得sinx，cosx，tanx，cotx为等差数列，

则应有于是有

两式相减得：tanx-cotx=sinx-cosx,

　①

❶若sinx-cosx=0，即sinx=cosx，此时这样就有：

tanx=cotx=1.故此时，sinx，cosx，tanx，cotx不成等差数列.

❷若sinx-cosx≠0，则在①式中约掉sinx-cosx之后，

得sinxcosx=sinx+cosx，而事实上，

∴在这种情况下，①式仍然不能成立.

综合❶❷可知，假设不成立，即不存在这样的x.

例3　一个袋中装有大小相同的黑球、白球和红球，已知袋中共有10个球，从中任意摸出1个球，得到黑球的概率是从中任意摸出2个球，至少得到1个白球的概率是求:(www.xing528.com)

(1)从中任意摸出2个球，得到的都是黑球的概率；

(2)袋中白球的个数.

解题策略　含有“至少”“至多”型的概率问题可以考虑用对立事件的概率求解.

解：(1)由题意知，袋中黑球的个数为

记“从袋中任意摸出2个球，得到的都是黑球”为事件A，则

(2)记“从袋中任意摸出2个球，至少得1个白球”为事件B.

设袋中白球的个数为x,则

解得x=5(舍去x=14).

所以袋中有5个白球.

例4　试求实数k的取值范围，使抛物线y=x2的所有弦都不能被直线y=k(x-3)垂直平分.

解题策略　本题共直接从正面解决，则条件“不能被直线垂直平分”较难用式子表示，正难则反，若我们先从问题的反面入手，化“不能”为“能”，则可快速求解，这也是补集思想的解题策略.必须注意的是中点P应落在y>x2的区域内或弦的两个端点存在，也即弦所在直线方程与抛物线方程联立，有两个相异的根.

解法一　设抛物线y=x2上两点关于直线y=k(x-3)对称，AB的中点为P(x0,y0),

则由题设知

且AB的中点P(x0,y0)在直线y=k(x-3)上，

因此中点

由于点P在y>x2的区域内，

整理得(2k+1)(6k2-2k+1)<0,解得

因此当时，抛物线y=x2上存在两点关于直线y=k(x-3)对称，

∴当时，抛物线y=x2上不存在两点关于直线y=k(x-3)对称.

故实数k的取值范围为

解法二　设抛物线上的两点关于直线y=k(x-3)对称，依题意知:

由此可得

于是，由得此时，抛物线上存在两点关于直线y=k(x-3)对称，从而所有弦不能被直线垂直平分的k的取值范围是