巧解数学问题：构造对偶式的技巧

在解答某些数学问题时，针对已知式M的结构特征，构造一个或几个与之相关联的式子N,使M与N经过相加、相减、相乘、相除等运算之后，所需解答的问题得到合理的转化和解决.这种解题方法称之为构造“对偶式”解题，是一种极其巧妙的解题方法.

通过构造对偶式可以巧妙地解决多项式求值、恒等式证明、求函数的最值、解方程(组)以及求解析式等，当然难点在于如何构造解题所需要的“对偶式”.

例1　求证：2sin4x+3sin2xcos2x+5cos4x≤5.

解题策略　本例是三角不等式的证明，运用一般的方法证明是困难的，若能运用对称的思想方法，构造对偶式，则比较容易证明.

证明　设A=2sin4x+3sin2xcos2x+5cos4x,

B=2cos4x+3cos2xsin2x+5sin4x,

则A+B=7(sin4x+cos4x)+6sin2xcos2x=7(sin2x+cos2x)2-8sin2xcos2x

=7-2sin22x=5+2cos22x　　①

A-B=3(cos4x-sin4x)=3cos2x　　②

①+②,得2A

所以A≤5，命题得证.

例2　已知α，β是方程x2-7x+8=0的两根，且α>β，不解方程，求的值.

解题策略　若要不解方程求+3β2的值，因为是非对称式，无法化为α+β及αβ的形式，所以需要构造相应的对偶式两者结合就可以化为α+β及αβ的形式，然后运用韦达定理，从而求出的值.

解：设构造对偶式

∵α，β是方程x2-7x+8=0的两根，∴α+β=7,αβ=8.

　　①

　　②

得

例3　求下列各式的值：

(1)sin210°+cos240°+sin10°cos40°；

(2)sin6°sin42°sin66°sin78°.

解题策略　本例两小题都可以通过三角恒等变形求值，但解题过程不简捷.如果利用正余弦三角函数的互余对偶，构造对偶式求解，则解题过程非常简捷，此时原问题转化为代数方程组，利用加减消元法获得结果，或两对偶式相乘结合诱导公式直接消去引进的对偶式即得结果.

解：(1)设A=sin210°+cos240°+sin10°cos40°,

另设B=cos210°+sin240°+cos10°sin40°,

则A+B=1+1+sin10°cos40°+cos10°sin40°=2+sin50°=2+cos40°.

两式相加，得即

因此，得

(2)设A=sin6°sin42°sin66°sin78°，

另设B=cos6°cos42°cos66°cos78°.

则AB(www.xing528.com)

即

例4　(1)若函数f(x)满足其中a，b，c是不等于零的常数，且|a|≠|b|，求函数f(x)的解析式；

(2)已知函数f(x)满足求f(x)的值域；

(3)已知an-1=nd,n∈N*,设求Sn+1.

解题策略　第(1)(2)两问，以代x,构造出与之对应的对偶式，联立方程组解出f(x).第(2)问还需用判别式法或基本不等式法进一步求f(x)的值域.第(3)问，构造对偶式(即写出原等式的逆序形式)，再利用组合数性质两式相加即可求得Sn+1.这也就是推导等差数列前n项和Sn的公式的方法——逆序相加法.

解：(1)用代替x，得原式的对偶式

联立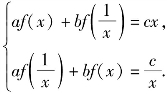消去得又∵|a|≠|b|.

(2)　　①

用代替x得①式的对偶式　　②

①×2+②得

　　③

求③的值域可用判别式法：

由

∵x∈R且

或即f(x)的值域为

也可用基本不等式：

当x>0时，即

当x<0时，则

即

∴f(x)的值域为

(3)由

构造对偶式(即原式逆序形式)，

则2Sn+1

运用组合数性质

=运用等差数列性质：在等差数列{an}中，若m，n，p，q∈N,且m+n=p+q，则am+an=ap+aq)

=(a0+an)·2n(运用二项展开式二项式系数之和的公式)

=(n+2)·2nd(运用等差数列通项公式).

∴Sn+1=(n+2)·2n-1d.