数形结合法解决平面向量问题

向量是既有大小又有方向的量，故向量具有代数和几何的双重身份，向量的引入给传统的数学带来了无限生机和活力，对向量的应用，要注意向量与平面几何的结合、向量与三角函数及解三角形的结合、向量与解析几何的结合及用空间向量解立体几何问题，用向量法解题体现了图形语言与符号语言的相互转换，要注意领悟其中包含的数形结合思想及思维方法.

向量加法的平行四边形(或三角形)法则是运用几何性质解决向量问题的基础，向量的坐标表示及坐标运算法则是用代数的方法来研究向量，体现了向量集数、形于一身的特点，还有诸如向量的模.而向量的夹角、共线与垂直都是“形中觅数、数中寻形”，代数问题几何化、几何问题代数化.

例1　(2016年高考数学天津卷理科第7题)已知△ABC是边长为1的等边三角形，点D，E分别是边AB,BC的中点联结DE并延长到点F，使得DE=2EF,则的值为(　　).

解题策略　本例考查平面向量的线性运算和数量积的运算，考查数形结合思想及运算求解能力，可以从不同的角度领会图形中向量运算的几何意义，从而得到多种解法.

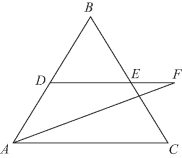
图5-78

解法一　如图5-78所示，设

根据已知得，

解法二　由向量数量积的几何意义知，为在上的投影与的乘积.

如图5-79所示，分别过A，F作BC的垂线，垂足为E,G，过D作DH⊥BC,垂足为H，则

解法三　如图5-80所示，以BC为x轴，BC的中垂线为y轴，建立平面直角坐标系，则

由得又故

图5-79

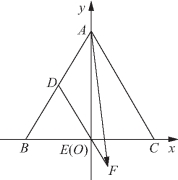
图5-80

例2　(1)已知△ABC的3个顶点的坐标满足如下条件：向量则∠AOB的取值范围是________;

(2)在平面上，若则的取值范围是(　　).

解题策略　第(1)问，点C是一个定点，点A是一个动点，而故点A在以点C为圆心，为半径的圆上运动，可以结合图形求解；第(2)问，根据条件找到相关各点构成的图形，建立平面直角坐标系，运用向量坐标法结合不等式知识求的取值范围.

解：(1)由可知，点A的轨迹是以C(2，2)为圆心，为半径的圆.

过原点O作此圆的切线，切点分别为M，N，如图5-81所示，联结CM,CN，则向量与的夹角θ的范围是∠MOB≤θ≤∠NOB.

由图可知∠COB=45°.

由知∠COM=∠CON=30°,

∴∠BOM=45°-30°=15°,∠BON=45°+30°=75°,∴15°≤θ≤75°,

即15°≤∠AOB≤75°.

(2)由条件知A，B1，P，B2构成一个矩形AB1PB2,以AB1，AB2所在直线为坐标轴建立直角坐标系(如图5-82所示)，设点O的坐标为(x,y)，则点P的坐标为(a,b).

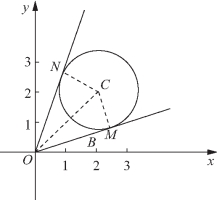
图5-81

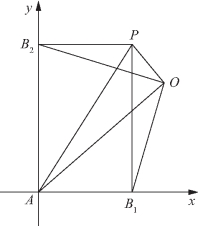
图5-82

由得

　　①

　　②

由①②知故选D.

例3　如图5-83所示，在Rt△ABC中，已知BC=a，若长为2a的线段PQ上点A为中点，向量与的夹角θ取何值时的值最大？并求出这个最大值.

解题策略　平面向量的数量积运算法则把平面向量与实数紧密地联系在一起，使它们之间的相互转化得以实施，解答本题的关键是结合图形，利用向量加减运算的三角形法则找出向量之间的关系，或建立适当的坐标系，利用向量的坐标运算来解答.因此，一方面我们要善于把向量的有关问题通过数量积转化为实数问题，利用实数的有关知识来解决问题；另一方面，也要善于把实数问题转化为向量问题，利用向量这个工具解决相关问题.

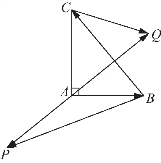
图5-83

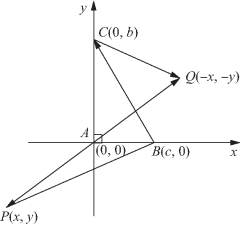
图5-84

解法一　

故当cosθ=1,即和的方向相同)时，最大，其最大值为0.

解法二　以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图5-84所示的平面直角坐标系.

设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.(www.xing528.com)

设点P的坐标为(x,y)，则Q(-x，-y)，

则

=(x-c)(-x)+y(-y-b)

=-(x2+y2)+cx-by.

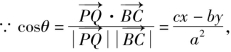
∴cx-by=a2cosθ.

故当cosθ=1,即和的方向相同)时，最大，其最大值为0.

例4　(1)已知圆O的半径为1，PA,PB为该圆的两条切线，A，B为两切点，那么的最小值是________;

(2)已知在平行四边形ABCD中，边AB,AD的长分别为2，1，若M，N分别是边BC,CD上的点，且满足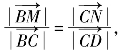则的取值范围是________.

解题策略　本例两小题是与向量数量积有关的最值或值域的求法.通常，对于向量的数量积的计算有3种方法：①利用向量数量积的定义，计算两个向量的模及夹角；②根据向量数量积的几何意义，明确向量投影的含义；③建立坐标系写出向量坐标，利用向量的坐标进行运算.而求最值或值域常用配方法、判别式法或基本不等式法求解.

解：(1)解法一　如图5-85所示，设PA=PB=x(x>0),∠APO=α,则cos2α

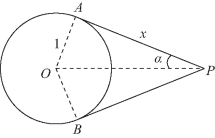
图5-85

=x2(1-2sin2α)

当且仅当即时等号成立，

的最小值是

解法二　同解法一得令则

即x4-(1+y)x2-y=0.

∵x2是实数，∴Δ=[-(1+y)]2-4×1×(-y)≥0,

即y2+6y+1≥0,解得或

故此时

解法三　设∠APB=θ,0<θ<π，

则

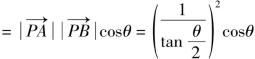
令则

(2)解法一　由向量数量积的定义得

∵M,N分别是边BC,CD上的点，∴可记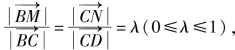

则

从而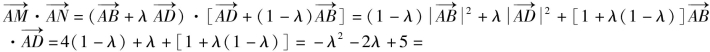-(λ+1)2+6(0≤λ≤1).

∴当λ=0时，取最大值5；当λ=1时，取最小值2.

解法二　如图5-86所示，以向量所在直线为x轴，以过点A垂直于AB的直线为y轴建立平面直角坐标系.

图5-86

设则

∴点M的坐标为

即

∴当时，取最大值5，当时，取最小值2.