利用三角函数的图像可以确定解析式中参数的值,研究三角函数的性质可以处理三角函数的定义域、值域、单调性、周期性、奇偶性、最值以及函数零点的个数等问题.
例1 (1)设x∈[0,2π],关于x的方程sinx+2|sinx|-k2+k=0有4个实根,则实数k的取值范围是________;
(2)函数![]() 的最大值是________,最小值是________;
的最大值是________,最小值是________;
(3)函数![]() 的定义域是________.
的定义域是________.
解题策略 第(1)问,转化为在x∈[0,2π]条件下求函数f(x)=sinx+2|sinx|与函数g(x)=k2-k图像的交点个数问题;第(2)问,结合斜率公式求动点与定点斜率的最大值、最小值;第(3)问,可借助三角函数的图像或单位圆中的三角函数线确定函数的定义域.
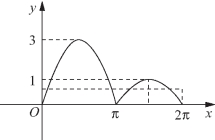
图5-68
解:(1)当x∈[0,2π]时,关于x的方程sinx+2|sinx|-k2+k=0可化为
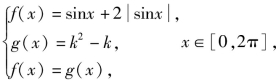
作出函数![]() 和g(x)=k2-k(0≤x≤2π)的图像,如图5-68所示.
和g(x)=k2-k(0≤x≤2π)的图像,如图5-68所示.
∵ 方程有4个实根,∴0<k2-k<1,
解得![]() 或
或![]()
∴实数k的取值范围是![]()
(2)解法一![]() 可以化为
可以化为![]() 设
设![]()
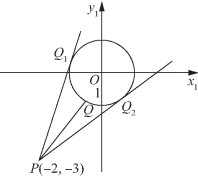
图5-69
则问题转化为求k的最大值、最小值.
构造点P(-2,-3)、Q(cosx,sinx),点Q的轨迹是单位圆![]() 如图5-69所示,切线PQ1、PQ2的斜率就是k的最大值、最小值.设直线PQ的方程为y1+3=k(x1+2),即kx1-y1+2k-3=0,由圆心到直线的距离等于半径,得
如图5-69所示,切线PQ1、PQ2的斜率就是k的最大值、最小值.设直线PQ的方程为y1+3=k(x1+2),即kx1-y1+2k-3=0,由圆心到直线的距离等于半径,得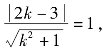 解得
解得![]()
∴y的最大值、最小值分别为ymax=![]()
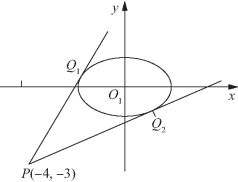
图5-70
解法二 如图5-70所示,构造两个点,即点P(-4,-3)和点Q(2cosθ,sinθ),这时![]() 点Q在椭圆
点Q在椭圆![]() 上.
上.
设直线PQ的方程为y1+3=k(x1+4),
即kx1-y1+4k-3=0,由直线和椭圆相切的条件易得![]()
∴函数的最大值和最小值分别为![]() 和
和![]()
(3)解法一 要使函数![]() 有意义,必须且只需
有意义,必须且只需
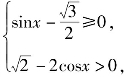 即
即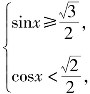 由y=sinx的图像(如图5-71所示)可知,使
由y=sinx的图像(如图5-71所示)可知,使![]() 的取值区间是
的取值区间是![]()
由y=cosx的图像(如图5-72所示)可知,使![]() 的取值区间是
的取值区间是![]()
∴函数![]() 的定义域为
的定义域为![]()
解法二 利用单位圆中的三角函数线(如图5-73所示)阴影部分为同时满足![]() 的x的取值范围.
的x的取值范围.
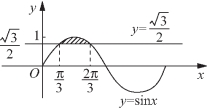
图5-71
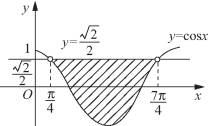
图5-72
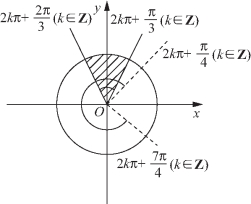
图5-73
由终边相同的角的表示可知函数的定义域为![]()
例2 求实数a的取值范围,使得对于任意![]() 恒有
恒有![]()
解题策略 本例用三角函数的方法直接解是困难的,如果把不等式左边看成两点距离的平方,则可以找到一种相当简捷的解法.
解:原不等式可看作点P(-3-2sinθcosθ,-asinθ-acosθ)与直线l:y=x上任意一点距离的平方大于等于![]()
由点P到直线l的距离公式得![]()
令![]()
则原不等式可化为![]()
结合t的取值范围可求得![]() 或
或![]() (https://www.xing528.com)
(https://www.xing528.com)
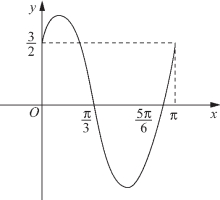
图5-74
例3 (1)若函数![]() 的图像如图5-74所示,求它的解析式、初相、周期与振幅;
的图像如图5-74所示,求它的解析式、初相、周期与振幅;
(2)求函数![]() 的周期;
的周期;
(3)设函数f(x)=Asin(ωx+φ)(A,φ,ω是常数,A>0,ω>0),若f(x)在区间![]() 上具有单调性,且
上具有单调性,且![]() 则f(x)的最小正周期为________.
则f(x)的最小正周期为________.
解题策略 第(1)问,由图像求三角函数y=Asin(ωx+φ)的解析式,进而求初相、周期、振幅.一看最高点、最低点的纵坐标,得出振幅A,若最高点、最低点未知,则看其他关键点,代入点的坐标,通过解方程组得解;二看图像反映的最小正周期,由![]() 得到ω的值;三看呈递增趋势的零点
得到ω的值;三看呈递增趋势的零点![]() 由ω的值求出初相φ,取点确定φ时,应取最高点或最低点,取其他点时要检验.第(2)问,如何求函数f(x)=f1(x)+f2(x)+…+fn(x)的周期?只要求出f1(x),f2(x),…,fn(x)的周期依次为T1,T2,…,Tn,则T1,T2,…,Tn的最小公倍数就是函数f(x)的一个周期.第(3)问,可从函数单调性入手将逆向思维的问题转化为正向思维的问题解决,还可充分挖掘图像的几何性质——对称性,以及对称性与周期性的关系,通过对图形的直觉观察寻找简捷的解法.
由ω的值求出初相φ,取点确定φ时,应取最高点或最低点,取其他点时要检验.第(2)问,如何求函数f(x)=f1(x)+f2(x)+…+fn(x)的周期?只要求出f1(x),f2(x),…,fn(x)的周期依次为T1,T2,…,Tn,则T1,T2,…,Tn的最小公倍数就是函数f(x)的一个周期.第(3)问,可从函数单调性入手将逆向思维的问题转化为正向思维的问题解决,还可充分挖掘图像的几何性质——对称性,以及对称性与周期性的关系,通过对图形的直觉观察寻找简捷的解法.
解:(1)解法一 ∵点![]() 在曲线上,
在曲线上,
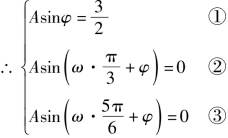 由②③得
由②③得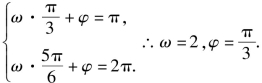
代入①式得![]()
∴解析式为![]() 初相
初相![]() 周期T=π,振幅
周期T=π,振幅![]()
解法二 由图知![]()
又图像过点![]()
又点![]() 在图像上,
在图像上,![]()
∴解析式为![]() 初相
初相![]() 周期T=π,振幅
周期T=π,振幅![]()
(2)设![]() 则y1的最小正周期T1=π;
则y1的最小正周期T1=π;
![]() 则y2的最小正周期
则y2的最小正周期![]() 的最小公倍数为2π,∴T=2π.
的最小公倍数为2π,∴T=2π.
(3)解法一 ∵f(x)在区间![]() 上具有单调性,且
上具有单调性,且![]()
![]() 和
和![]() 均不是f(x)的极值点,其极值应该在
均不是f(x)的极值点,其极值应该在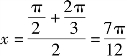 处取得.
处取得.
又![]() 也不是函数f(x)的极值点.
也不是函数f(x)的极值点.
又f(x)在区间![]() 上具有单调性,
上具有单调性,![]() 为f(x)的另一个相邻的极值点,故函数f(x)的最小正周期
为f(x)的另一个相邻的极值点,故函数f(x)的最小正周期![]()
解法二 由f(x)在区间![]() 具有单调性,且
具有单调性,且![]() 可知函数f(x)的一个对称中心为
可知函数f(x)的一个对称中心为![]() 由
由![]() 知函数f(x)的一条对称轴为直线
知函数f(x)的一条对称轴为直线![]() 由f(x)在区间
由f(x)在区间![]() 上具有单调性可得
上具有单调性可得![]()
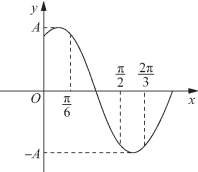
图5-75
解法三 由已知画出图像(如图5-75所示),结合图像得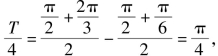
∴T=π.
例4 (1)在长方体ABCD-A1B1C1D1中,求证:
![]()
(2)设x,y,z∈(0,1),求证:x(1-y)+y(1-z)+z(1-x)<1.
解题策略 这两小题都是不等式的证明,从表面看似乎与三角函数关系不大.如果我们能从不等式中找到某种几何模型,原问题就转化为三角函数问题,运用三角知识求解.事实上,第(1)问的几何模型是给出的,不等式中的三个角实质上是长方体的一条体对角线与从同一个顶点出发的三条面对角线所成的角,借助这个图形,运用一系列的三角恒等变形即可证得结果;第(2)问,联想到面积公式,通过构造三角形,利用图形进行直观转化,使得该题解法妙趣横生.
证明 (1)画出长方体ABCD-A1B1C1D1如图5-76所示.
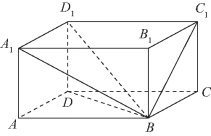
图5-76
❶设∠A1BD1=α,∠DBD1=β,∠C1BD1=γ,则α,β,γ均为锐角,且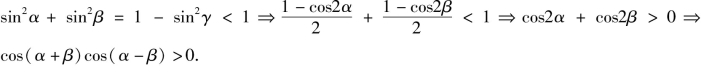
![]()
同理![]() 故
故![]()
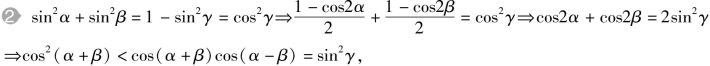 由
由![]() 故
故![]()
由❶ ❷得![]()
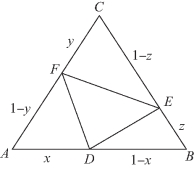
图5-77
(2)原不等式等价于![]()
联想到三角形面积公式,构造三角形,利用已知图形的性质进行直观转化,如图5-77所示,作边长为1的正三角形ABC,在边AB,BC,CA上分别取点D,E,F,使AD=x,BE=z,CF=y,则DB=1-x,CE=1-z,AF=1-y.
∵S△FAD+S△DBE+S△CEF<S△ABC(局部小于整体),
![]()
∴x(1-y)+y(1-z)+z(1-x)<1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




