数形结合：解函数零点问题

运用数形结合的思想解函数零点(方程根)的问题，即把函数零点(方程根)的问题通过转化看作两个函数图像交点问题，借助函数图像，采用直观分析的方法，通过研究交点问题来研究、判断或求解函数零点(方程根)的个数以及图像交点横坐标之和，对于函数零点(方程根)存在的情况下求参数之和，要特别注意相应函数的性质，如奇偶性、单调性、周期性以及图像的对称性在解函数零点(方程根)问题中的作用.

例1　(1)(2018年高考数学天津卷理科第14题)

已知a>0，函数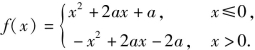若关于x的方程f(x)=ax恰有2个互异的实数解，则a的取值范围是________;

(2)(2018年高考数学全国Ⅰ卷理科第9题)

已知函数若g(x)存在2个零点，则a的取值范围是(　　).

A.[-1,0)　　　B.[0,+∞)　　　C.[-1,+∞)　　　D.[1,+∞)

解题策略　第(1)问，主要考查函数的零点、利用零点个数求参数的取值范围，考查的核心素养是直观想象和逻辑推理.通常研究方程根的情况，可以通过构造函数，研究函数的单调性、最值、图像的变化趋势等求解.根据题目要求，画出函数图像，通过数形结合思想去分析问题，可以使问题的求解有一个清晰、直观的整体展现.本题可以针对x≤0和x>0直接构造分段函数，利用图像法求解，也可以参变分离构造函数结合导数知识及数形结合求解，第(2)问，破解此类题的关键：一是会转化，先把函数的零点问题转化为方程根的问题，再转化为两个函数图像的交点问题；二是会借形解题，即作出两函数的图像，数形结合可快速找到参数所满足的不等式，解不等式即可求出参数的取值范围.

解：(1)解法一　当x≤0时，由x2+2ax+a=ax得a=-x2-ax；

当x>0时，由-x2+2ax-2a=ax得

令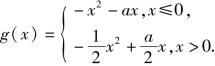则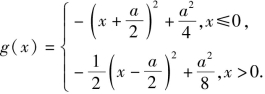

作出直线y=a与函数g(x)的图像，如5-60(a)所示.

若f(x)=ax恰有2个互异的实数解，则且

∴a<8且a>4.∴4<a<8.

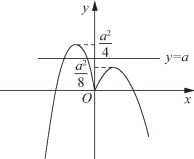
图5-60(a)

图5-60(b)

解法二　当x≤0时，由x2+2ax+a=ax得

a=-x2-ax;

当x>0时,由-x2+2ax-2a=ax,得2a=-x2+ax，

令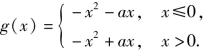作出直线y=a,y=2a，函数g(x)的图像如图5-60(b)所示，

g(x)的最大值为

若f(x)=ax恰有2个互异的实数解，则得4<a<8.

解法三　当x≤0时，由f(x)=ax得x2+2ax+a=ax,

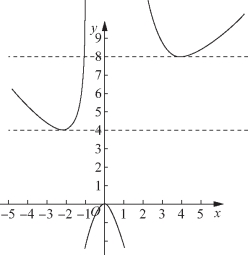
图5-60(c)

得x2+ax+a=0,得a(x+1)=-x2,得

设则

由g′(x)>0得-2<x<-1或-1<x<0，此时递增，

由g′(x)<0得x<-2,此时递减，即当x=-2时，g(x)取得极小值为g(-2)=4,

当x>0时，由f(x)=ax得-x2+2ax-2a=ax,

得x2-ax+2a=0,得a(x-2)=x2;

当x=2时，方程不成立;

当x≠2时，

设则

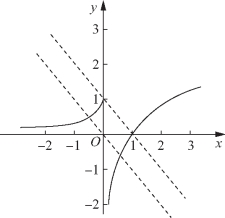
图5-61

由h′(x)>0得x>4，此时递增，

由h′(x)<0得0<x<2或2<x<4,此时递减，即当x=4时，h(x)取得极小值为h(4)=8,要使f(x)=ax恰有2个互异的实数解，则由图5-60(c)知4<a<8,故答案为(4,8).

(2)函数g(x)=f(x)+x+a存在2个零点，即关于x的方程f(x)=-x-a有2个不同的实根，即函数f(x)的图像与直线y=-x-a有2个交点，作出直线y=-x-a与函数f(x)的图像，如图5-61所示，由图可知，-a≤1,解得a≥-1,故选C.

例2　(1)已知函数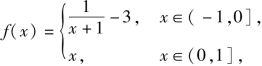且g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点，则实数m的取值范围是(　　).

(2)定义在R上的奇函数f(x),当x≥0时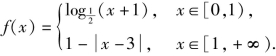，则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为(　　).

A.2a-1　　　B.2-a-1　　　C.1-2-a　　　D.1-2a

解题策略　第(1)问，函数g(x)=f(x)-mx-m的零点个数问题就是曲线y=f(x)和动直线y=m(x+1)的交点个数问题，需要画出函数图像，利用数形结合思想直观判断出交点个数，而y=f(x)是分段函数，要注意自变量的取值范围，即在函数的定义域内画图，再利用直线y=m(x+1)过定点(-1，0)，通过转动直线判断何时有两个交点，利用分界点处直线的斜率求解范围.第(2)问，先画出当x≥0时，f(x)的图像，再根据f(x)在R上是奇函数，其图像关于原点对称补上x≤0的图像.并在同一坐标平面内画上直线y=a(0<a<1),可以直观地看到两图像交点的个数，根据对称性，很容易求出所有零点之和.

解：(1)g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点⟺函数y=f(x)的图像与函数y=m(x+1)的图像在(-1,1]内有两个交点，在同一直角坐标系内作出函数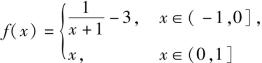和函数y=m(x+1)的图像，如图5-62所示.

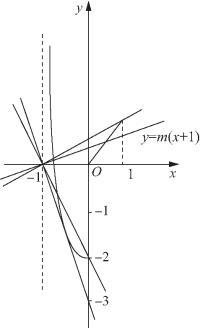
图5-62

当直线y=m(x+1)与和y=x,x∈(0,1]都相交时，

当直线y=m(x+1)与有两个交点时，由方程组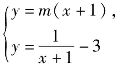消元得即m(x+1)2+3(x+1)-1=0,化简得mx2+(2m+3)x+m+2=0,当Δ=9+4m=0,即m=时，直线y=m(x+1)与相切，当直线y=m(x+1)过点(0，-2)时，m=-2,

综上，实数m的取值范围是故选A.

(2)当-1≤x<0时，1≥-x>0;x≤-1时，-x≥1,(www.xing528.com)

又f(x)为奇函数，

∴x<0时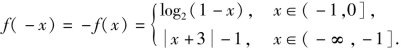，画出y=f(x)和y=a(0<a<1)的图像如图5-63所示，共有5个交点，设其横坐标从左到右分别为x1，x2，x3，x4，x5，则而log2(1-x3)=ax3=1-2a.

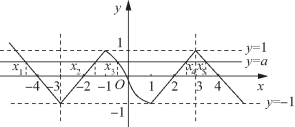
图5-63

可得x1+x2+x3+x4+x5=1-2a，故选D.

例3　(1)定义域为R的偶函数f(x)满足对∀x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时，f(x)=-2x2+12x-18，若函数y=f(x)-loga(|x|+1)在(0，+∞)上至多有3个零点，则a的取值范围是(　　).

(2)(2017年高考江苏卷理科第14题)设f(x)是定义在R上且周期为1的函数，在区间[0,1)上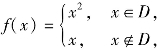，其中集合则方程f(x)-lgx=0的解的个数是________.

解题策略　第(1)问，首先利用f(x)是偶函数的条件求出f(1)，进而得到函数具有周期性，然后利用函数的周期性和奇偶性作出函数f(x)的图像，利用y=f(x)与y=loga(|x|+1)的图像在(0,+∞)上至多有三个交点确定a的取值范围.第(2)问,解题的基本方法同样是利用数形结合，将函数的零点问题转化为两个函数图像的交点个数问题，关键是根据题设的信息正确作出f(x)的图像.

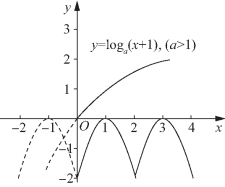
图5-64

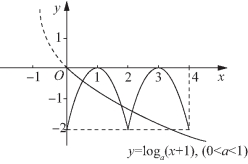
图5-65

解：(1)∵函数f(x)是偶函数，∴令x=-1，得f(-1+2)=f(-1)-f(1)=f(1),解得f(1)=0.

∴f(x+2)=f(x)-f(1)=f(x),即函数的周期是2.

由y=f(x)-loga(|x|+1)=0得f(x)=loga(|x|+1),令y=loga(|x|+1),

当x>0时,y=loga(|x|+1)=loga(x+1),

函数图像过点(0，0).

❶若a>1时，则由图像(如图5-64所示)可知，此时函数y=f(x)-loga(|x|+1)在(0,+∞)上没有零点，

∴此时满足条件.

❷若0<a<1，则由图像(如图5-65所示)可知，要使两个函数y=f(x)与y=loga(|x|+1)在(0,+∞)上至多有3个交点，则y=loga(|x|+1)不能在点B(4，-2)上方，即

综上所述，满足条件的a的取值范围是故选B.

(2)由于f(x)∈[0,1)，因此只需考虑1≤x<10的情况.

在此范围内，x∈Q且x∉Z时，设且p，q互质，

若lgx∈Q,则由lgx∈(0,1)，可设且m,n互质，

因此则此时左边为整数，右边非整数，矛盾，

因此lgx∉Q.

故lgx不可能与每个周期内x∈D对应的部分相等，

只需考虑lgx与每个周期内x∉D部分的交点.

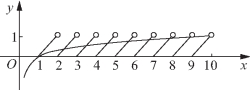
图5-66

画出函数草图(如图5-66所示)，图中交点除(1，0)外其他交点横坐标均为无理数，属于每个周期x∉D的部分，且x=1处

则在x=1附近，仅有一个交点，

因此方程f(x)-lgx=0的解的个数为8.

例4　已知a，b是实数，1和-1是函数f(x)=x3+ax2+bx的两个极值点.

(1)求a和b的值；

(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点；

(3)设h(x)=f(f(x))-c,其中c∈[-2,2],求函数y=h(x)的零点的个数.

解题策略　本题的难点在第(3)问，探讨函数h(x)=f(f(x))-c,c∈[-2,2]零点的个数，根据函数零点的定义可知，函数h(x)的零点就是方程h(x)=0的实根，因此判断一个函数是否有零点，有几个零点，就是判断方程h(x)=0是否有实根，有几个实根，但通常用代数法，即求方程h(x)=0的实根的方法比较困难，应当运用几何法，即与y=h(x)的图像联合起来，并利用函数的性质找出零点，但是本题直接作出y=h(x)的图像还是困难，必须进一步转化对c的取值分类讨论确定函数y=h(x)的零点个数.

解：(1)由题意得，1和-1是方程f′(x)=3x2+2ax+b=0的两个零点，

∴a=0,b=-3.

(2)由(1)得f(x)=x3-3x,g′(x)=x3-3x+2=(x-1)2(x+2),

函数y=g′(x)的零点为-2.∴g(x)的极值点为-2.

(3)要求函数y=h(x)的零点个数，即求f(f(x))=c的实根个数，

即求f3(x)-3f(x)=c的实根个数，作示意图如图5-67所示，

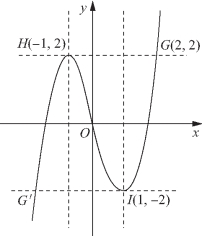
图5-67

❶当c=2时,f(x)=-1或2,f(x)=-1有3个解,f(x)=2有2个解，

故函数y=h(x)的零点个数为5；

❷当c=-2时，同理可得，函数y=h(x)的零点个数为5；

❸当-2<c<2时，f(x)有三个解，分别是t1∈(-2,-1),t2∈(-1,1),t3∈(1,2).

由于f(x)=ti各有3个解，所以函数y=h(x)的零点个数为9.

综上所述，当|c|=2时，函数y=h(x)有5个零点；当|c|<2时，函数y=h(x)有9个零点.