数形结合：深入研究函数性质

运用数形结合思想解函数问题的着眼点是利用函数图像的直观性.探求解题途径，主要体现在利用函数图像研究函数的性质、比较函数值的大小.求函数的最值以及求参数范围等.

例1　(1)设a，b，c均为正数，且则a，b，c从小到大的排列顺序为________；

(2)已知函数y=f(x)的反函数为y=f-1(x),又方程f(x)+x-2=0与f-1(x)+x-2=0的实数解分别为α与β，则α+β的值为________.

解题策略　构造相应函数解析式，作出图像，由图像比较值的大小或求相应值之和.

解：(1)由题意分别画出函数的图像，如图5-44所示.可得a<b<c.

(2)∵α是方程f(x)=2-x的解，

∴α是两函数y=f(x)与y=2-x图像的交点A的横坐标.

同理，β是函数y=f-1(x)与y=2-x图像的交点B的横坐标.

函数y=f(x)与y=f-1(x)的图像关于直线y=x对称，

又A，B都在直线y=2-x上，而且直线y=2-x与y=x垂直，

所以A，B两点关于直线y=x对称，即A，B两点的纵、横坐标是一种互换关系，

所以点A的坐标为(α，β)，它在直线y=2-x上，

如图5-45所示，β=2-α,即α+β=2.

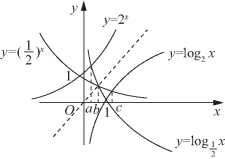
图5-44

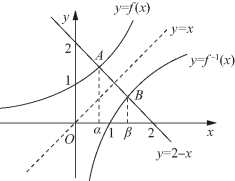
图5-45

例2　(1)已知函数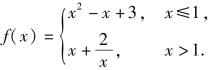设a∈R，若关于x的不等式在R上恒成立，则a的取值范围是(　　).

(2)已知函数f(x)=x(1+a|x|),设关于x的不等式f(x+a)<f(x)的解集为A，若则实数a的取值范围是(　　).

解题策略　第(1)问主要考查分段函数与不等式恒成立问题，意在考查化归与转化能力、运算求解能力以及分类讨论思想，在处理含参不等式恒成立问题时，要充分利用函数的图像求解.第(2)问主要考查函数的单调性、二次函数性质，考查数形结合思想、分类讨论思想，解题的关键是将f(x)写成分段函数，再对影响图像开口方向的字母a分类讨论，结合图像将转化为关于a的不等式，解之即得结果.

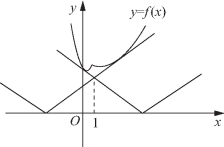
图5-46

解：(1)根据题意，作出f(x)的大致图像如图5-46所示，以函数f(x)的图像之“静”制约函数图像之“动”，函数的图像可由函数的图像经过平移生成.当a<0时向右平移-2a个单位，当a>0时向左平移2a个单位，在平移过程中必须保证函数的图像始终在函数f(x)图像的“下方”(可有重合点)，由图像不难发现在移动的过程中f(x)的图像的“左段”与函数的图像(折线)的左支相切是极限状态，即当x≤1时，若要恒成立，结合图像，只需即故对于方程4(3+a)≤0,解得当x>1时，若要恒成立，结合图像，只需即又当且仅当即x=2时等号成立，∴a≤2.

综上，a的取值范围是故选A.

(2)易知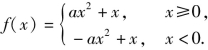

❶当a>0时，作出f(x)的图像如图5-47所示，可知f(x)单调递增，

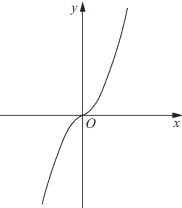
图5-47

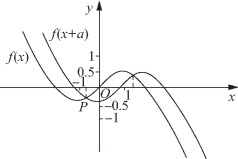
图5-48

∴f(x+a)<f(x)⟺x+a<xa<0,矛盾！

❷当a<0时，作出f(x)，f(x+a)的图像如图5-48所示.

令即点P的横坐标为

由及图像可知：

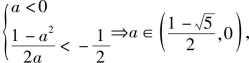故选A.

例3　(1)设非空集合A={x|-2≤x≤a},B={y|y=2x+3,且x∈A},C={z|z=x2且x∈A},若C⊆B,求实数a的取值范围；

(2)当时不等式2x-logax<0恒成立，求实数a的取值范围.

解题策略　第(1)问，由于a为参变数，所以定义域范围是变动的，z=x2的定义域右端点x=a有3种不同的位置情况，在讨论C⊆B时必须分类求解；第(2)问，分别作出函数y=2x及y=logax的图像，利用图像的形象性、直观性来分析解决问题.

解：(1)∵函数y=2x+3在[-2,a]上是单调递增函数，

∴-1≤y≤2a+3,即B={y|-1≤y≤2a+3}.

作出z=x2的图像，如图5-49所示.该函数定义域右端点x=a有3种不同的位置情况：

图5-49(www.xing528.com)

❶当-2≤a<0时，a2≤z≤4,即C={z|a2≤z≤4}，见图5-49(a).

要使C⊆B，需2a+3≥4，得与-2≤a<0矛盾;

❷当0≤a≤2时，0≤z≤4,即C={z|0≤z≤4}，见图5-49(b).

要使C⊆B,必须且只需解得

❸当a>2时,0≤z≤a2,即C={z|0≤z≤a2}，见图5-49(c).

要使C⊆B,必须且只需解得2<a≤3.

综上所述，a的取值范围是

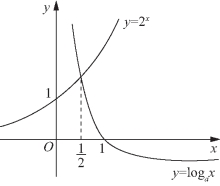
图5-50

(2)要使不等式2x<logax在时恒成立，即函数y=logax的图像在内恒在函数y=2x图像的上方，而y=2x的图像过点由图5-50可知，显然这里0<a<1.

∴函数y=logax在(0,+∞)上是减函数，又即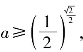

故所求a的取值范围为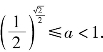

例4　已知函数在区间[-1,1),(1,3]上各有一个极值点.

(1)求a2-4b的最大值；

(2)当a2-4b=8时，设函数y=f(x)在点A(1,f(1))处的切线为l，若l在点A处穿过函数y=f(x)的图像(即动点在点A附近沿曲线y=f(x)运动，经过点A时，从l的一侧进入另一侧)，求函数f(x)的表达式.

解题策略　选择图像的特殊点(即三次函数的对称中心——拐点)来精心设计试题，是本题在设计上的一个创新点，解题时需要深入分析图像特征，利用导数来求解，在解题过程中有时并非一定要作图，但一定要心中有图，由函数的性质思考图像的走向，这是非常重要的数学核心素养.

解：(1)解法一　∵函数在区间[-1,1),(1,3]上分别有一个极值点，∴f′(x)=x2+ax+b=0在[-1,1),(1,3]上分别有一个实根，设两实根为x1,x2(x1<x2),则且0<x2-x1≤4.于是

且当x1=-1,x2=3,即a=-2,b=-3时等号成立.

故a2-4b的最大值是16.

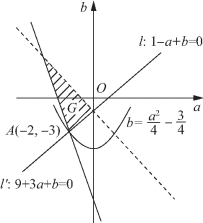
图5-51

解法二在[-1,1),(1,3]上分别有一个实根，原问题等价于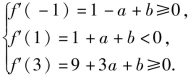

作出可行域G如图5-51所示，令S=a2-4b,

得寻求其几何意义，可得抛物线过点A(-2,-3)时纵截距取最小值，即Smax=a2-4b=(-2)2-4×(-3)=16.

(2)解法一　由f′(1)=1+a+b知，f(x)在点A(1,f(1))处的切线l的方程是y-f(1)=f′(1)(x-1),即

∵切线l在点A(1，f(1))处穿过y=f(x)的图像，

在x=1两边附近的函数值异号，则x=1不是g(x)的极值点.

而

则g′(x)=x2+ax+b-(1+a+b)=x2+ax-a-1=(x-1)(x+1+a),

若1≠-1-a,则x=1和x=-1-a都是g(x)的极值点,

∴1=-1-a,即a=-2.

又由a2-4b=8,得b=-1,故

解法二　同解法一得

∵切线l在点A(1,f(1))处穿过y=f(x)的图像，

∴g(x)在x=1两边附近的函数值异号，于是存在m1,m2(m1<1<m2)满足：

当m1<x<1时，g(x)<0；当1<x<m2时，g(x)>0;

或当m1<x<1时,g(x)>0；当1<x<m2时,g(x)<0.

设则有以下结论：

h(x)在x=1左右两侧同号，即

当m1<x<1时，h(x)>0;当1<x<m2时,h(x)>0;

或当m1<x<1时,h(x)<0;当1<x<m2时,h(x)<0.

由h(1)=0结合h(x)的结构特征(抛物线开口向上)知，x=1是h(x)的一个极值点，

则得a=-2;

又由a2-4b=8,得b=-1,故